15^e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels

Date limite: 31 décembre 2000.

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14.
• Catégorie GP (grand public): problèmes 5 à 14.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16.
• Catégorie HC (haute compétition): problèmes 5 à 16.

Énoncés des problèmes

Début catégorie CM

1 - Les dix verres (coefficient 1)

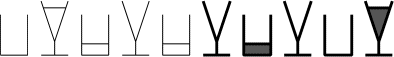
Dix verres sont sur le comptoir. Trois contiennent du jus de pomme (de couleur claire) et deux contiennent du jus de raisin (de couleur foncée). Mais la distribution a été mal faite. Seuls les cinq verres les plus à droite (en traits plus épais) doivent contenir du jus de fruits, les cinq verres les plus à gauche devant être vides. De plus, deux verres de même forme doivent toujours contenir la même sorte de jus de fruits. Une manipulation consiste à prendre un verre, à le vider dans un verre vide, puis à le remettre à sa place initiale. Combien de manipulations seront-elles nécessaires, au minimum, pour parvenir à ce résultat?

2 - La caravane Peugeot (coefficient 2)

L'autre jour, sur la route, se succédaient des voitures Peugeot d'années très différentes: une 106, une 203 et une 309. J'ai alors pensé à d'autres modèles de la même marque: 204, 304, 404, 504, 604. Parmi tous les nombres cités, on peut en trouver quatre dont la somme est égale à celle de trois autres. Quel est le nombre qui reste seul?

Début catégorie C1

3 - Rangement pénible (coefficient 3)

Combien peut-on ranger, au maximum, de pièces en forme de croix dans une boîte rectangulaire 11 × 8?
Note: les pièces, rangées à plat, peuvent se toucher, mais pas se superposer.

4 - Parois pivotantes (coefficient 4)

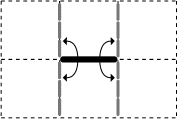
Pour une exposition de jeux mathématiques, Thomas a disposé 15 panneaux en spirale (disposition 1). Nina préfèrerait la disposition 2. Chaque panneau peut pivoter autour de ses extrémités (voir figure ci-contre). Quel nombre de parois faut-il faire pivoter, au minimum, pour passer d'une disposition à l'autre?

Début catégories C2 L1 GP L2 HC

5 - Aïe mes aïeux (coefficient 5)

La femme de D. Sandent a accouché de trois garçons en l'an 1800 (un beau triplé!). Depuis, chaque individu Sandent de sexe masculin a eu lui-même 3 garçons, sauf un petit-fils de D. Sandent et un arrière petit-fils de D. Sandent qui n'ont pas eu d'enfant. Je suis moi-même le dernier né (de sexe masculin) de la 7^e génération suivant D. Sandent. Au fait, combien de descendants de D. Sandent (de sexe masculin) ont-ils porté son nom, de la 1^re à la 7^e génération?

6 - Les sept disques (coefficient 6)

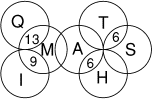
Les 7 disques Q, I, M, A, T, H, S ont chacun une valeur différente comprise entre 1 et 7. Dans certaines intersections de deux disques, on a indiqué la somme des valeurs de ces deux disques. Quelle est la somme des valeurs des cinq disques M, A, T, H, S?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le champ du Père Méable (coefficient 7)

Pierre Méable possède un champ carré de 100 m de côté. Amateur de fleurs, il a partagé son champ en quatre bandes de même largeur, il a tracé une diagonale, puis il a planté une partie du champ en rosiers (en gris sur le dessin) et le reste en tulipes. Quelle fraction du terrain représente la partie plantée en rosiers?

8 - Les cinq nombres (coefficient 8)

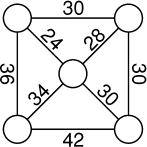
Cinq nombres étaient écrits sur les cinq disques du dessin ci-contre. Ils ont été effacés, mais heureusement, sur chaque segment, on avait pris soin de noter la somme des deux nombres placés dans les deux disques situés aux extrémités de ce segment. Retrouvez les cinq nombres.
Correction: pour le nombre le plus à droite, il faut lire 36 et non 30.

9 - Billes en tête (coefficient 9)

Jacques a six sacs de billes devant lui. Les nombres de billes contenues dans les sacs sont des entiers consécutifs pas nécessairement distincts, par exemple comme 12, 12, 13, 14, 14, 15. Jacques prend trois sacs pour lui et donne les trois autres à son frère. Il possède alors 58 billes en tout et son frère en a 61. Donnez par ordre croissant les nombres de billes contenues dans les sacs.

Fin catégorie C1

10 - Quelle famille (coefficient 10)

Des membres d'une même famille sont réunis pour un anniversaire. Parmi les personnes présentes, il y en a deux qui peuvent être appelées papa par au moins une autre personne de l'assemblée, deux qui peuvent être appelées maman, deux mon fils, deux ma fille, deux ma soeur, quatre mon frère, deux ma belle-soeur, deux mon beau-frère, deux ma cousine, deux mon cousin, deux ma nièce, deux mon neveu, deux ma tante, deux mon oncle, deux ma femme et deux mon mari. Combien de personnes sont-elles présentes, au minimum? Note: On supposera que lorsque deux personnes quelconques sont en présence l'une de l'autre, chacune ne peut appeler l'autre que d'une seule façon.

11 - Un château médiéval (coefficient 11)

Le château de Mathville est entouré d'un rempart de hauts murs. Ces murs mesurent, classés par ordre croissant, 10 m, 20 m, 30 m, 40 m, 50 m, 60 m, 80 m, 110 m. D'autre part, chaque mur est perpendiculaire au mur précédent et au mur suivant.
Quelle est, au maximum, l'aire du domaine intérieur au mur d'enceinte? Vous donnerez la réponse en dam².

Fin catégorie C2

12 - Esprit de suite (coefficient 12)

8 7 5 6 3 5 3 0 1 8 ....... On a choisi et écrit deux chiffres: le 8 et le 7, puis on a écrit leur produit 56. Ensuite, on écrit le produit du 7 (2^e chiffre) et du 5 (3^e chiffre): 35, puis le produit du 5 (3^e chiffre) et du 6 (4^e chiffre): 30. On continue ainsi en se décalant d'un rang à chaque fois et en écrivant à la suite le produit des deux chiffres considérés (qui s'écrit avec un ou deux chiffres). Au bout d'un temps plutôt long, on n'obtiendra que des zéros. Quel sera le dernier chiffre non nul?

13 - Mi-carré - mi-cube (coefficient 13)

Un nombre est dit mi-carré - mi-cube s'il peut s'écrire comme la somme d'un carré et d'un cube. Ainsi, l'an 2000 aura été une année mi-carrée - mi-cube car 2000 = 44² + 4³. Quelle était la précédente année mi-carrée - mi-cube?

14 - La petite grenouille et les pavés (coefficient 14)

La petite grenouille est capable de sauter d'un seul bond par dessus les 20 pavés. Mais elle peut aussi aller de D à A en se posant sur un ou plusieurs pavés intermédiaires. Les seules règles qu'elle s'est imposées à elle-même sont d'aller toujours en avant et de ne jamais sauter d'un pavé à un autre pavé immédiatement adjacent. Combien de parcours différents peut-elle effectuer pour aller de D à A?

Fin catégories L1 GP

15 - Cadres autoréférents (coefficient 15)

Cadre A --------->	Le cadre A contient .............................. lettres de moins que le cadre B.
Cadre B --------->	Le cadre B contient .............................. lettres de moins que le cadre C.
Cadre C --------->	Le cadre C contient .............................. lettres de moins que n'en contiennent les cadres A et B ensemble.

Complétez les pointillés avec des nombres écrits en toutes lettres afin que toutes les phrases écrites dans les cadres soient vraies.

16 - Le cerf-volant aux 4 lunules (coefficient 16)

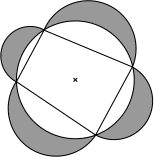
Le cadre de ce cerf-volant est un quadrilatère inscrit dans un cercle. Les côtés du quadrilatère mesurent des nombres entiers de centimètres tous différents. Pour des raisons aérodynamiques, quatre lunules sont fixées sur le cadre, chacune d'elles ayant pour diamètre le côté du quadrilatère sur lequel elle est attachée. La somme des aires des quatre lunules (en gris) est égale à celle du quadrilatère. Quelle est-elle, au minimum?
On donnera la réponse en cm².

Fin catégories L2 HC