15e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 12 mai 2001
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Achat en gros
(coefficient 1)
- Le pack de six bouteilles de jus d'orange coûte
42 F, alors que la bouteille
à l'unité coûte 7,80 F.
Mathilde doit acheter 20 bouteilles pour son anniversaire.
Combien dépensera-t-elle, au minimum?
- 2 - La trottinette de Mathias
(coefficient 2)
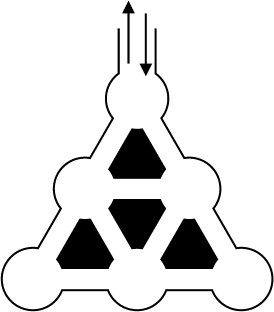
Mathias vient de recevoir en cadeau une superbe trottinette. Il décide
de l'essayer sur le trottinodrome
représenté ci-contre. Mais
les pneus, encore neufs, laissent une trace sur le bitume de la piste.
Mathias parcourt chaque allée exactement une fois. Il peut repasser
par le même carrefour, mais la trace qu'il laisse ne doit jamais se
recouper. Dessinez un trajet possible.
Début catégorie C1
- 3 - La toile de Gipsy
(coefficient 3)
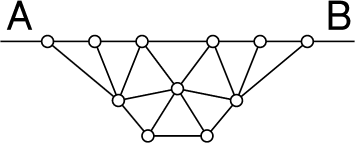
Le dessin représente la toile de l'araignée Gipsy. Une goutte de rosée
est suspendue à chaque intersection. Cette toile énerve la libellule
Myria, qui décide de la détruire. Myria coupe des segments de toile,
toujours entre deux gouttes de rosée. Mais elle n'est pas très maligne
et elle a coupé un peu au hasard. D'ailleurs, après l'attaque de Myria,
Gipsy peut encore se déplacer sur ses fils pour aller de A à B.
Combien de segments Myria a-t-elle pu couper, au maximum?- 4 - Vive les mariés!
(coefficient 4)
- Les parents de Mathilde veulent ranger les 250 plus belles photos
de leur mariage dans des albums. Un album se compose de 12 pages, chacune
pouvant contenir 8 photos. Combien de photos la dernière page utilisée
contiendra-t-elle?
Début catégories C2 L1 L2 GP HC
- 5 - Parc d'attractions
(coefficient 5)
- Julien et Denis ont passé la journée à Math-Land. Le midi, ils ont
chacun pris un sandwich et une boisson. À la buvette, on leur a proposé
de choisir: sandwich au jambon (7 F),
au fromage (11 F) ou au saumon
(14 F), et, en boisson, il y avait
du lait (6 F), du jus d'orange
(7 F) ou une boisson aux fruits
exotiques (9 F). Julien a dépensé
6 F de plus que Denis.
Combien Denis a-t-il dépensé?
- 6 - Mur de couleur
(coefficient 6)

Ce mur est construit à partir de briques de couleurs jaune, brune et
rouge. Deux briques qui se touchent sont toujours de couleurs différentes.
Les briques jaunes valent 6 F,
les rouges 7 F et les brunes
8 F.
À combien ce mur reviendra-t-il, au minimum?
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Tomber sur un os
(coefficient 7)
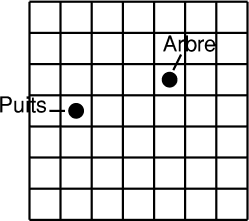
L'os d'Hexane est enterré quelque part dans le terrain rectangulaire
ci-contre, constitué de parcelles carrées.
Tout ce que l'on sait, c'est que le triangle formé par le puits,
l'arbre et l'os est un triangle rectangle isocèle.
Noircissez tous les petits carrés où peut se trouver l'os
d'Hexane.- 8 - Le siège de la FFJM
(coefficient 8)
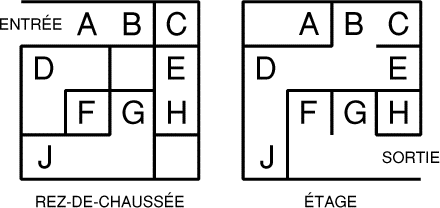
Voici les plans du futur siège de la FFJM. Le dessin
de gauche représente le rez-de-chaussée et le dessin de droite représente
le 1er étage. Les ascenseurs sont désignés par des lettres (à
chaque lettre, on peut prendre l'ascenseur ou continuer). On veut aller
de l'entrée à la sortie par le chemin le plus court. Indiquez, dans
l'ordre, la liste des ascenseurs utilisés.- 9 - Le pré Ventif
(coefficient 9)

Isidore-Noël Ventif veut partager le terrain représenté ci-contre en cinq
parcelles de même aire et de même forme (éventuellement retournable).
Aidez I.-N. Ventif à faire le partage.
Fin catégorie C1
- 10 - Le collage de Mathilde
(coefficient 10)
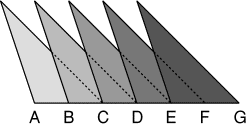
À l'aide de cinq triangles de forme et de dimensions identiques, Mathilde
vient de réaliser un magnifique collage (non figuratif). Les points B, C,
D, E, F sont les milieux respectifs des côtés [AC], [BD], [CE], [DF] et
[EG]. Chaque grand triangle a une aire égale à
0,95 dm².
Quelle est l'aire du collage tout entier?- 11 - Le magnétoscope de Denis
(coefficient 11)
- Il est 20 heures. Le magnétoscope de Denis indique 4 heures du
matin, mais c'est normal, car il est déréglé: son horloge avance de
15% plus vite qu'une horloge normale. Quel horaire Denis doit-il
programmer pour enregistrer son émission préférée qui commence demain
à 16 h 40?
Fin catégorie C2
- 12 - Tout pareil!
(coefficient 12)
- Les outils toujours affûtés, Gilles s'amuse à dessiner un rectangle
et un losange.
Il s'aperçoit alors que ses deux quadrilatères ont non seulement le même
périmètre, mais aussi la même aire.
De plus, les longueurs des côtés du rectangle et des diagonales du losange
sont des nombres entiers de centimètres.
Quel est le plus petit périmètre possible du rectangle de
Gilles?
- 13 - Les trapèzes
(coefficient 13)
- Combien existe-t-il de trapèzes (non croisés) différents de
périmètre égal à 11 cm et dont
les côtés ont tous des longueurs entières (en
cm)? Note: on considérera comme
identiques deux trapèzes se déduisant l'un de l'autre par une rotation
ou par une symétrie.
- 14 - Le redresseur de codes
(coefficient 14)
- L'agent 007 doit effectuer une mission dans un département français
dont le code comprend deux chiffres. Le premier chiffre est codé par la
suite 2587193460 7X et le second par la suite 0491329000 00.
Chacun de ces deux codes est constitué de dix chiffres (choisis entre 0
et 9 inclus) suivis d'une clé à deux chiffres appartenant à l'ensemble
{0;1;2;3;4;5;6;7;8;9;X} où X correspond au nombre 10. Le premier chiffre
de la clé doit être le reste de la division par 11 de la somme des dix
premiers chiffres du code, et le second chiffre de la clé doit être égal
au reste de la division par 11 de la somme des produits des dix premiers
chiffres par leur rang dans le code. Chacun des deux codes ci-dessus
comporte un symbole volontairement erroné. Les deux symboles corrects
qui remplacent ces deux symboles erronés donnent le code du département.
Quel est ce code?
Fin catégories L1 GP
- 15 - Un vrai petit bijou
(coefficient 15)
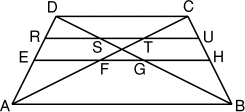
Agathe a gagné au Championnat Féminin des Jeux Mathématiques un bijou
en argent. Ce bijou a la forme d'un trapèze isocèle ABCD de bases
56 mm et
84 mm, incrusté de deux fils d'or
[EH] et [RU] parallèles aux bases. Si on traçait les diagonales [AC] et
[BD], celles-ci partageraient les deux fils d'or en trois segments égaux
EF = FG = GH et RS = ST = TU.
Quelle est la somme des longueurs des deux fils d'or incrustés?
Si besoin est, on donnera la réponse arrondie au centième de
millimètre.- 16 - Duo de chocolats
(coefficient 16)

Cette nouvelle tablette de chocolat est constituée de douze carrés de
chocolat noir et de douze carrés de chocolat blanc. Les carrés de chocolat
noir sont tous solidaires: on peut passer de n'importe quel carré noir à
n'importe quel autre carré noir par une chaîne de carrés noirs se touchant
par un côté, et il en est de même des carrés blancs. De plus, la forme des
carrés noirs est parfaitement superposable à celle des carrés blancs (à un
retournement près).
Le fabricant veut réaliser tous les modèles possibles.
Combien en existe-t-il?
Note: on considérera comme identiques deux modèles se déduisant l'un de
l'autre par une symétrie ou par une rotation.
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org








