14^e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 13 mai 2000

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - De 1 à 5 (coefficient 1)

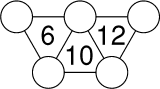
Placez les nombres de 1 à 5 dans les cercles. La somme des nombres situés aux sommets de chaque triangle est indiquée dans le triangle.

2 - La petite grenouille (coefficient 2)

Une petite grenouille se trouve au bas d'un escalier composé de 21 marches. Elle bondit sur la 2^ème marche, puis continue à grimper par bonds de 2 marches. Mais les marches portant les numéros 5, 10, 15 et 20 sont glissantes et, lorsqu'elle arrive sur l'une d'elles, elle redescend d'une marche en glissant.
Combien de bonds la petite grenouille doit-elle faire pour atteindre la 21^ème marche?

Début catégorie C1

3 - Des tas de bonbons (coefficient 3)

Mathias possède entre 39 et 49 bonbons. Il les dispose en tas de 9 bonbons et constate alors qu'il lui reste autant de bonbons qu'il a réalisé de tas.
Combien la boîte contenait-elle de bonbons, exactement?

4 - La marelle de Marielle (coefficient 4)

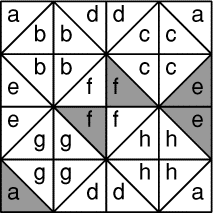
Marielle a dessiné une marelle faite de petits carrés divisés en triangles. Elle veut colorier certains triangles de façon que:

• dans chaque petit carré, il y ait un triangle coloré et un triangle blanc;
• parmi les quatre triangles portant la même lettre, il y ait deux triangles colorés et deux triangles blancs.

Elle a commencé à colorier certains triangles (en gris sur le dessin). Aidez Marielle à terminer son coloriage en respectant les consignes.

Début catégories C2 L1 L2 GP HC

5 - Le dé de Bill (coefficient 5)

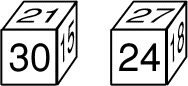
Bill, qui n'est pas bête, possède un dé un peu particulier, dont deux positions différentes sont représentées ci-contre. Les nombres sont disposés de telle sorte que la différence entre les nombres portés sur deux faces opposées est toujours la même. Quel est le nombre écrit sur la face opposée à celle portant le nombre 21?

6 - Le compte est bon (coefficient 6)

Dans la grille ci-contre, on entre par la case numérotée 1 et on sort par la case numérotée 9. On ne peut se déplacer qu'horizontalement ou verticalement, et il est interdit de passer deux fois par la même case. En passant par les cases 1-2-5-8-9, la somme obtenue est égale à 25. Mais tous les chemins ne conduisent pas forcément à un total de 25.
Donnez, de la plus petite à la plus grande, les neuf autres sommes réalisables.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le partage du Pays Plan (coefficient 7)

Mathilde dessine dans le Pays Plan cinq routes droites de façon que trois des cinq routes se croisent en un même endroit et que trois des cinq routes soient parallèles. En combien de régions ces cinq routes partagent-elles le Pays Plan?

8 - Tous les chemins mènent à Rome (coefficient 8)

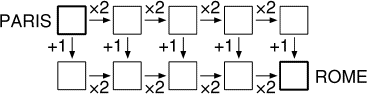
On passe d'une case à la suivante:

• en multipliant par 2 si on se déplace vers la droite;
• en ajoutant 1 si on se déplace vers le bas.

On ne peut aller ni vers le haut, ni vers la gauche. On part de Paris avec 1 et on parcourt tous les chemins possibles de Paris à Rome.
Quelle est la somme de tous les nombres obtenus à Rome?

9 - Cercle sur l'échiquier (coefficient 9)

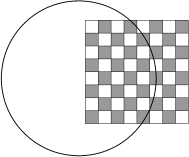
Mathias a dessiné un échiquier sur une feuille de papier. Il prend ensuite son compas et trace un cercle qui passe à l'intérieur de plusieurs cases de l'échiquier (le dessin montre un exemple où le cercle traverse 11 cases de l'échiquier). Si Mathias choisit bien le centre et le rayon de son cercle, combien de cases peut-il traverser, au maximum?

Fin catégorie C1

10 - Les trois randonneurs (coefficient 10)

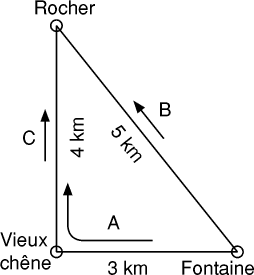
Trois randonneurs se déplacent sur le circuit pédestre représenté ci-contre, chacun marchant toujours dans le même sens, comme indiqué sur la figure, et à vitesse constante. Albert et Béatrice marchent à la même vitesse, tandis que Camille marche deux fois plus vite. Albert et Béatrice sont partis à 10 heures de la fontaine, et Camille à 11 heures du vieux chêne, juste au moment où Albert y passait.
À quelle heure Béatrice et Camille se rencontreront-elles pour la première fois?

11 - Le février des 5 jeudis (coefficient 11)

Quelle sera la prochaine année où le mois de février comptera cinq jeudis? Note: Nous sommes le samedi 13 mai 2000.

Fin catégorie C2

12 - 2000 rectangles pour l'an 2000 (coefficient 12)

Pour fêter l'an 2000, Léonard a réalisé un beau dessin. Pour cela, il a tout d'abord dessiné un grand rectangle sur une feuille de papier. Il a ensuite partagé ce rectangle en traçant des lignes joignant les côtés opposés du rectangle et perpendiculaires à ceux-ci. Il a enfin peint les différents rectangles obtenus.
Tu as vu, dit-il à son père, il y a exactement 2000 rectangles.
C'est vrai si on ne compte que les rectangles élémentaires, mais si on compte tous les rectangles possibles, alors il y en a beaucoup plus!, lui répond celui-ci.
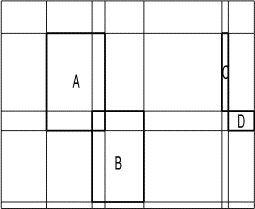
Combien le dessin de Léonard compte-t-il de rectangles, au maximum? Note: On appelle rectangle élémentaire un rectangle qui n'est pas traversé par une ligne, comme les rectangles C et D de l'exemple, les rectangles A et B n'étant pas élémentaires.

13 - Audrey cherche la lumière (coefficient 13)

Audrey entre dans une pièce non éclairée et munie de trois interrupteurs numérotés 1, 2 et 3, dont elle ne connaît pas les états. Chaque interrupteur peut être ouvert ou fermé, et pour que la pièce soit éclairée, il faut qu'ils soient tous les trois fermés.
Audrey appuie sur l'interrupteur n° 1; la pièce ne s'éclaire pas.
Audrey appuie ensuite sur l'interrupteur n° 2; la pièce ne s'éclaire toujours pas. Elle cherche alors une stratégie qui lui permette d'éclairer la pièce en un nombre minimum d'essais. En appliquant cette stratégie, quelle séquence d'interrupteurs Audrey doit-elle actionner, dans le pire des cas?

14 - Le jeu numérique (coefficient 14)

Mathilde et Mathias jouent avec les nombres de l'ensemble {2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}. Mathilde commence en écrivant un premier nombre choisi dans cet ensemble. C'est ensuite au tour de Mathias, qui choisit un autre nombre de l'ensemble, le multiplie par le nombre déjà écrit, et inscrit le produit. Chacun, ensuite, à tour de rôle, choisit dans l'ensemble un nombre non encore choisi, le multiplie par le dernier nombre écrit, puis inscrit le produit. Le premier joueur qui doit écrire un nombre plus grand que 1000 a perdu.
Quel nombre doit jouer Mathilde pour être sûre de gagner, quel que soit le jeu de son adversaire?
Répondez 0 solution si vous pensez qu'il n'existe pas de stratégie gagnante pour Mathilde.

Fin catégories L1 GP

15 - La patrouille (coefficient 15)

Les motards Francis, Gilles, Matthieu, Joseph et Michel patrouillent sur une route de 120 km de long. Chacun patrouille sur un segment et un seul de cette route.
Francis et Gilles patrouillent dans deux moitiés différentes.
Francis, Gilles et Matthieu patrouillent dans trois tiers différents.
Francis, Gilles, Matthieu et Joseph patrouillent dans quatre quarts différents.
Enfin, Francis, Gilles, Matthieu, Joseph et Michel patrouillent dans cinq cinquièmes différents.
Quelle est, au minimum, la longueur totale des segments de cette route sur lesquels aucun motard ne patrouille?
Si besoin est, on arrondira au kilomètre le plus proche.

16 - Les 36 pommiers (coefficient 16)

Trente-six pommiers étaient disposés en carré comme sur la figure. La tempête en a abattu un certain nombre, mais parmi ceux qui restent debout, trois arbres ne sont jamais alignés.
Combien en reste-t-il, au maximum? Vous donnerez une disposition correspondant à ce maximum.
N.d.V.L.: le jour de l'épreuve, il y avait un emplacement pour le nombre de solutions, mais il n'était finalement pas demandé.

Fin catégories L2 HC