13e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels
Date limite: 31 décembre 1998; 29 janvier 1999 (heure locale) pour le Québec; 31 janvier 1999 pour la Belgique.
Ne pas diffuser les réponses avant le 1er février 1999.
Catégories
Énoncés des problèmes
Début catégorie CM
- 1 - Les longueurs
(coefficient 1)
- Combien de longueurs différentes existe-t-il entre
les points du réseau ci-contre?

- 2 - Le code des TTP
(coefficient 2)
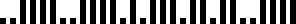
Les enveloppes des lettres destinées à la ville dont le code postal
est 0 2 1 0 0 portent la bande représentée ci-dessus.
Quel est le code postal de la ville pour laquelle la bande est la
suivante:
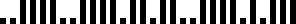
Début catégorie C1
- 3 - Le dé voyageur
(coefficient 3)
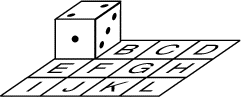
Les 12 cases d'un damier de 4 cases sur 3 sont désignées par les lettres
de A à L. On pose un dé normal
sur la case A. On doit ensuite
faire basculer le dé autour d'une de ses arêtes pour l'amener sur une
case voisine de celle qu'il occupait, et on peut répéter cette opération
en changeant ou non l'arête autour de laquelle le dé pivote.
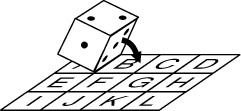
On veut amener le dé de la case A à la case L en cinq mouvements. On choisit
la position de départ du dé (elle peut être différente de celle représentée
sur le dessin) et on additionne les nombres de points portés par les cases
en contact avec le damier, de la première case (la case A) à la sixième case
(la case L).
Quel est le plus grand total que l'on puisse obtenir?
On rappelle que sur un dé normal
, deux cases opposées portent des
nombres dont la somme vaut 7.- 4 - La classe de Mathilde
(coefficient 4)
- Dans la classe de Mathilde, il y a deux groupes: les fans des
Moutarde Girls
et ceux des 3 C'est 4
. Tout le monde
appartient à l'un des deux groupes et personne n'appartient aux deux
à la fois. Chacun des deux groupes compte un nombre impair de membres
(entre 10 et 20), et l'un des deux surpasse l'autre de quatre unités.
Par ailleurs, dans la classe de Mathilde, il y a deux fois plus de
filles que de garçons.
Combien y a-t-il de filles, Mathilde comprise, dans cette
classe?
Début catégories C2 L1 GP L2 HC
- 5 - Les billes de Mathias
(coefficient 5)
- Mathias a dans son sac 30 billes de trois couleurs. Il sait que s'il
retire de son sac 25 billes choisies au hasard, il y aura parmi elles au
moins 3 billes blanches, au moins 5 bleues et au moins 7 vertes.
Combien le sac de Mathias contient-il de billes bleues?
- 6 - Petit déjeuner
(coefficient 6)
- Ce matin, pour le petit déjeuner, il y avait deux cruches identiques,
l'une remplie de café et l'autre remplie de lait. Chaque membre de la
famille s'est servi et a bu 125 millilitres de café au lait, après avoir
fait le mélange selon les proportions qui lui conviennent.
Mathias s'est servi le premier. Il a bu le quart de la cruche de lait et le
sixième de la cruche de café. Après que le dernier membre de la famille se
fut servi, il restait moins de 125 ml
dans les deux cruches réunies. Combien de personnes, Mathias compris,
compte cette famille?
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Le terrain du Père Siffleur
(coefficient 7)
- Le Père Siffleur possède un terrain carré représenté ci-contre,
dont le côté mesure un nombre entier d'hectomètres. Il décide de partager
son terrain en quatre parcelles rectangulaires. Les trois premières
parcelles ont des aires respectives de
18 hm²,
27 hm² et
72 hm².

Quelle est l'aire de la quatrième parcelle?
- 8 - La chaîne tricolore
(coefficient 8)

Francis a trouvé trois fragments de chaîne. Les chaînons sont de trois
couleurs: bleus (notés 1), blancs (notés 2) et rouges (notés 3). Francis
aimerait bien constituer une chaîne unique dans laquelle les chaînons
seraient bleu, blanc, rouge, bleu, blanc, rouge, et ainsi de suite
jusqu'au dernier chaînon rouge. Pour cela, il doit obligatoirement
ouvrir et refermer quelques chaînons!
Sachant qu'il met 30 secondes pour ouvrir un chaînon et 30 secondes
pour le refermer, quelle est la durée minimale nécessaire pour constituer
une chaîne tricolore de 12 chaînons?- 9 - Le pousse-pousse de Francine
(coefficient 9)
- Francine s'est fabriqué un petit pousse-pousse dans lequel elle a
inscrit son nom (dessin n°1). Une amie malicieuse s'est amusée à mélanger
l'ordre des lettres en les faisant glisser un peu au hasard, mais sans les
sortir de la boîte (dessin n°2).
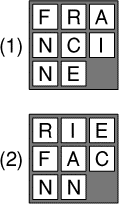
Francine demande en combien de coups au minimum il est possible de
rétablir son nom.
Attention, un coup
peut être le déplacement d'une ou de deux
lettres dans une même direction, avec le pouce! Ainsi, si on descend
les lettres E et C, cela ne compte que pour un coup.
Fin catégorie C1
- 10 - Cryptarithme
(coefficient 10)
J E U
+ U M E
---------
= F F J M
Comme dans tout cryptarithme, deux lettres différentes représentent
toujours deux chiffres différents, et deux chiffres différents sont
toujours représentés par deux lettres différentes. De plus, aucun
nombre ne commence par un zéro.
Trouvez le nombre de solutions et donnez-en deux.- 11 - Le champ des six reines
(coefficient 11)
- Le vieil Ulysse possède un champ ayant la forme du dessin ci-contre.
Il veut le partager entre ses 6 filles, qu'il se plaît à appeler ses
petites reines. Chaque part doit avoir la même surface et la même forme à
un retournement près.
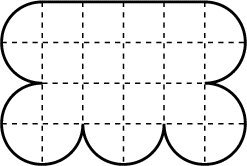
Faites le partage du champ des six reines.
Fin catégorie C2
- 12 - Les quadrilatères
(coefficient 12)
- Combien de quadrilatères différents, non superposables, même
avec retournement, peut-on tracer en utilisant quatre points du réseau
ci-contre?

note: Tous les types de quadrilatères, croisés ou non, sont envisagés
à l'exception des quadrilatères aplatis.
- 13 - Les dominos
(coefficient 13)
-
Deux joueurs, Bernard et Gilles, s'affrontent sur le tableau représenté
ci-dessus. Le jeu consiste à déposer à tour de rôle un domino qui doit
recouvrir exactement deux cases contiguës libres. Le premier joueur ne
pouvant plus jouer est perdant.
Bernard commence, mais Gilles a, en contrepartie, le privilège de pouvoir
limiter le nombre de cases du tableau, qui comptera un nombre de cases
compris, au sens large, entre 2 et 11. Quel nombre de cases doit choisir
Gilles pour être sûr de gagner, quel que soit le jeu de son adversaire?
Répondez 0 si vous pensez qu'il n'existe aucun choix gagnant pour
Gilles.
- 14 - Le jouet de Francis
(coefficient 14)
- Francis vient de recevoir pour son anniversaire un modèle réduit de
voiture radiocommandé. Celui-ci ne peut se déplacer qu'en marche avant,
soit en ligne droite, soit sur des arcs de cercle de rayon
63 cm. Francis essaie son nouveau
jouet au milieu d'un immense parking désert. Sa voiture se trouve en A,
orientée vers le Nord.
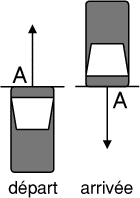
Quelle distance minimale Francis doit-il faire parcourir à son jouet
pour qu'il se retrouve en A, orienté vers le Sud?
On prendra 22 / 7 pour π.
Fin catégories L1 GP
- 15 - Les dés de la FFJM
(coefficient 15)

Quatre dés tétraédriques, parfaitement équilibrés, portent sur leurs faces
les lettres F, F, J, M (un patron d'un des dés est représenté ci-contre).
On lance quatre fois ces quatre dés.
Déterminez la probabilité pour que les quatre faces cachées indiquent
au moins une fois F, F, J, M. On donnera la réponse sous forme d'une
fraction irréductible.- 16 - Le fossile de l'année
(coefficient 16)
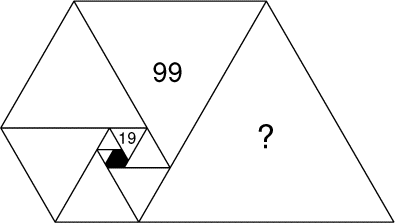
Le fossile de l'année est composé de dix triangles équilatéraux disposés
comme sur le dessin. Le côté de chaque triangle mesure un nombre entier de
millimètres. Deux de ces triangles, signalés sur le dessin, ont des côtés
mesurant respectivement 19 mm et
99 mm. Donnez la mesure, exprimée
en mm, du côté du plus grand triangle du
fossile de l'année.
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org