13^e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 15 mai 1999

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Voisin - voisine (coefficient 1)

La classe de Cours Moyen est composée de 25 élèves. La salle comporte 16 tables à deux places.
Combien d'élèves, au maximum, le professeur peut-il asseoir seuls à une table?

2 - Neuf-neuf (coefficient 2)

Mathias écrit les nombres entiers dans l'ordre, sans aucune séparation, à partir de 1:
1234567891011121314151617181920212223...
Il s'arrête dès qu'il a écrit deux 9 qui se suivent.
Combien de fois a-t-il écrit le chiffre 9?

Début catégorie C1

3 - Les pains d'épices de Prosper (coefficient 3)

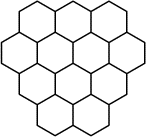
Prosper a acheté deux pains d'épices pour le goûter de Mathias et de Mathilde. Chacun d'eux partage son pain d'épices en trois parts de même forme, en suivant les lignes du dessin. Mais avant de manger chacun une part de son pain d'épices, ils remarquent que ces deux parts n'ont pas la même forme (même si on les retourne).
Dessinez deux découpages du pain d'épices en trois parts de même forme, de telle sorte que les parts du premier découpage et les parts du second aient des formes différentes.

4 - Les sept notes (coefficient 4)

Jean-Christophe et Gilles sortent du cours de maths.
J.-C.: Regarde mes sept notes du trimestre; elles sont toutes différentes: 4; 12; 6; 18; 9; 3; 15. C'est curieux, chaque note est soit un diviseur, soit un multiple de la précédente.
G.: Pour moi aussi, les sept notes sont toutes différentes, et chaque note est aussi soit un diviseur, soit un multiple de la précédente. Mais, bien que je n'aie jamais eu zéro, ma meilleure note, qui est aussi la dernière, est seulement 8. Donnez les sept notes de Gilles dans l'ordre où il les a obtenues.

Début catégories C2 L1 L2 GP HC

5 - L'église de Bernardswiller (coefficient 5)

L'église de Bernardswiller sonne toutes les quinze minutes, de la manière suivante:

• un quart d'heure après chaque heure pleine, elle sonne une fois trois coups;
• une demi-heure après chaque heure pleine, elle sonne deux fois trois coups;
• trois quarts d'heure après chaque heure pleine, elle sonne trois fois trois coups;
• à chaque heure pleine, elle sonne quatre fois trois coups, plus un coup à 01 h 00 et à 13 h 00, plus deux coups à 02 h 00 et à 14 h 00, ..., et plus douze coups à midi et à minuit.

Odile s'est éveillée juste avant que ne sonnent les coups de minuit, elle a passé vingt-quatre heures consécutives à travailler devant son écran d'ordinateur et elle s'est endormie, épuisée, juste après avoir entendu sonner à nouveau les coups de minuit.
Combien de coups Odile a-t-elle entendu sonner?

6 - Les petites différences (coefficient 6)

On dispose les nombres de 1 à 10 sur un cercle de telle sorte que la différence entre deux nombres voisins soit toujours égale à 2 ou à 3.
Dessinez une telle disposition.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le coco de Pedro (coefficient 7)

Pedro possède un perroquet savant: Jacquot, qui sait compter jusqu'à 8, mais qui est très capricieux.
Lorsque Pedro place des graines dans son écuelle, Jacquot en mange huit, puis il jette au sol les deux suivantes. Il recommence ensuite à en manger huit et jette au sol les deux suivantes. Il continue de la même manière, jusqu'à ce qu'il ne reste plus rien dans l'écuelle.
Dimanche, Pedro a nettoyé la pièce, puis il a placé des graines dans l'écuelle de Jacquot. Ce dernier mange comme à son habitude. Lundi, Pedro ramasse les graines jetées par terre et les remet dans l'écuelle. Mardi, il fait de même. Mercredi matin, il constate qu'aucune graine ne reste au sol.
Quel est le nombre maximum de graines placées par Pedro dans l'écuelle de Jacquot?

8 - Le jeu des pions (coefficient 8)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Bernard et Gaston jouent au jeu suivant.
Ils disposent d'une bande de 15 carrés numérotés de 1 à 15 et de 15 pions dans une boîte. Au départ, aucun pion n'est posé sur la bande. Bernard et Gaston jouent à tour de rôle. Bernard commence. À chaque coup, il peut prendre au plus 6 pions dans la boîte et les poser sur les cases libres de son choix. Gaston, lui, à chaque fois que c'est son tour de jouer, peut enlever de la bande un nombre quelconque de pions (au minimum un pion) à condition qu'ils soient sur des cases consécutives. Il doit alors les remettre dans la boîte.
En combien de coups, au minimum, Bernard peut-il poser tous les pions sur la bande, quel que soit le jeu de Gaston? Répondez 0 si vous pensez qu'une telle stratégie n'existe pas pour Bernard.

9 - Boîtes homogènes (coefficient 9)

Béatrice dispose de 3 boîtes contenant respectivement 576 billes, 212 billes et 211 billes. La seule opération autorisée pour modifier ces nombres est de prendre une bille dans deux boîtes et de mettre ces deux billes dans la troisième. Béatrice veut rendre sa répartition la plus homogène possible, c'est-à-dire qu'elle veut rendre la somme des écarts (positifs) entre les contenus des boîtes prises deux à deux la plus petite possible.
En combien d'opérations peut-elle y parvenir, au minimum?

Fin catégorie C1

10 - La ronde des lettres (coefficient 10)

  a b c d e f
         ×  4
-------------
= f a b c d e

Dans cette multiplication, les lettres a, b, c, d, e et f représentent six chiffres différents (a ne représente pas 0).
Retrouvez le nombre abcdef.

11 - Le dépôt de livres (coefficient 11)

Ce dépôt de livres est divisé en secteurs numérotés.

1. Les colis entreposés dans un même secteur ont tous la même masse, qui est un nombre entier de kilogrammes.
2. Pour n'importe quel secteur excepté le dernier, si l'on ajoute la masse de deux colis de ce secteur et celle d'un colis du secteur suivant, on trouve toujours 80 kg.
3. S'il y avait un secteur de plus, il serait impossible que les conditions (1) et (2) soient respectées.

Donnez la masse d'un colis du premier secteur de ce dépôt.

Fin catégorie C2

12 - Le jeu de Jean (coefficient 12)

Jean a inventé le jeu suivant.
Il écrit 1, qui est son premier nombre, puis 2, qui est son deuxième nombre. À chaque étape suivante, il choisit entre le double du dernier nombre écrit et la somme des deux derniers nombres écrits, et il inscrit le nombre choisi. Son but est que le seizième nombre écrit soit un nombre impair le plus grand possible.
Quel nombre peut-il atteindre?

13 - Les arithmégones (coefficient 13)

Un polygone convexe (dont tous les angles sont saillants) a la particularité suivante: si on écrit dans l'ordre croissant la suite des mesures en degrés de ses différents angles, on obtient une suite arithmétique de raison 20° (c'est-à-dire que la différence entre deux mesures consécutives est toujours égale à 20°).
Quelle est la mesure en degrés du plus petit angle?

14 - Le Dudeney (coefficient 14)

En 1905, le ludologue Henri Ernest Dudeney inventa un découpage du triangle équilatéral en quatre pièces permettant de reconstituer un carré. Le puzzle^* représenté ci-contre en est une version approchée, qui permet seulement de reconstituer un rectangle.

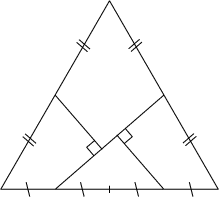
Que vaut le rapport (longueur / largeur) de ce rectangle?
Si besoin est, on prendra 1,732 pour √3 et on donnera une valeur arrondie au millième du résultat.
^* Ce puzzle est fabriqué par l'Atelier Archimédia (Lausanne) et diffusé par les Éditions Archimède (Argenteuil).

Fin catégories L1 GP

15 - Partage de l'espace (coefficient 15)

Quel est le plus petit nombre possible de plans appartenant à trois directions et permettant de partager l'espace de telle façon que le nombre de parties non bornées soit le double du nombre de parties bornées?

16 - Le meilleur point d'observation (coefficient 16)

Sur le diamètre [KN] d'un cercle de rayon 10 cm, on a mis une cloison composée de deux segments [KL] et [MN] tels que KL = 2 cm et MN = 15 cm (voir figure).

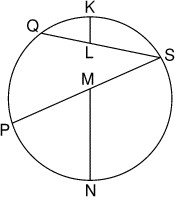
À partir des points du demi-cercle de droite, on observe les arcs situés sur le demi-cercle de gauche.
Quelle est la plus grande longueur d'arc observable?
Si besoin est, on prendra 3,1416 pour π et on donnera un résultat exprimé en cm, éventuellement arrondi au millième.

Fin catégories L2 HC