13e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 2e séance, 28 août 1999
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Défilé de majorettes
(coefficient 1)
- Fin août, à Gambetteville, a lieu chaque année un grand rassemblement
de majorettes. Lors du défilé, alors qu'elles regardent dans la même
direction et qu'elles profitent d'un moment de répit, Sophie et Marie
échangent quelques mots:
_ il y a deux rangs devant moi
, dit Sophie
_ il y a quatre colonnes à ma gauche
, répond
Marie
_ il y a dix rangs derrière moi
, dit Sophie
_ il y a cinq colonnes à ma droite
, termine
Marie.
Sachant que le défilé forme un superbe rectangle, de combien de
majorettes est-il constitué?
- 2 - Dans le cinq
(coefficient 2)
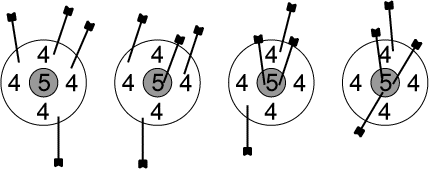
Les flèches plantées dans les cibles ci-dessus totalisent, de gauche à
droite, 16 points, 17 points, 18 points et 19 points. Avec un plus grand
nombre de flèches, on peut réaliser n'importe quel score plus grand que
19. Pourtant, il est impossible de réaliser un score de 1 point.
Quels sont les 5 autres scores qu'on ne peut pas obtenir?
Début catégorie C1
- 3 - Une famille moderne
(coefficient 3)
- Évariste et Sophie ont eu, chacun de leur côté, des enfants. Après
leur rencontre et leur mariage, ils ont eu d'autres enfants ensemble.
Aujourd'hui, tous réunis, ils sont dix à table pour fêter un anniversaire.
Évariste, qui est le père de six d'entre eux. a fait un beau gâteau. Sophie,
qui est la mère de sept d'entre eux, a coupé équitablement le gâteau.
Mais combien d'enfants Évariste et Sophie ont-ils eu ensemble?
- 4 - La brosse à dents de Mathilde
(coefficient 4)

Mathilde vient de s'acheter une brosse à dents en crins de cheval répartis
en 28 touffes qui ne contiennent pas toutes le même nombre de crins.
L'emballage indique: 600 crins
. La touffe indiquée par la flèche
est une de celles qui en contiennent le plus. Combien cette touffe
contient-elle de crins au minimum?
Début catégories C2 L1 L2 GP HC
- 5 - Les six enfants de Si. Bémol
(coefficient 5)
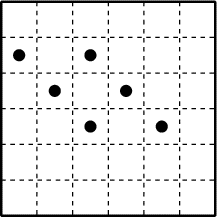
Le vieux Sigismond Bémol, surnommé Si. Bémol, possédait un terrain
planté de six figuiers. À sa mort, il a fallu partager son terrain entre
ses six enfants: Simon, Simone, Cyril, Sidonie, Sylvain et Sissi. Mais le
partage s'est compliqué lorsque chacun des enfants a exigé une parcelle
contenant un figuier et qui soit de même forme que celle de ses frères et
soeurs. Aidez le notaire à faire le partage.- 6 - Nombres à retrouver
(coefficient 6)
 |
A |
B |
C |
D |
|---|
| 2 |
oui |
oui |
oui |
oui |
|---|
| 3 |
oui |
oui |
oui |
oui |
|---|
| 4 |
non |
oui |
oui |
oui |
|---|
| 5 |
non |
non |
oui |
non |
|---|
| 7 |
non |
non |
non |
non |
|---|
| 9 |
oui |
oui |
non |
oui |
|---|
Nina a répondu à la question: est-il un multiple de
par un
tableau.
Les nombres A, B, C, D ont été effacés, mais Nina se souvient que
les nombres A, B, C, D étaient classés du plus petit au plus grand
et qu'ils étaient plus petits que 100. Aidez Nina à retrouver
ces nombres.
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - La frise qui défrise
(coefficient 7)
- Thomas a découpé quarante formes identiques à celle représentée
ci-contre.
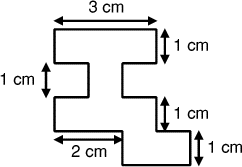
Il a commencé à les assembler en une frise régulière.
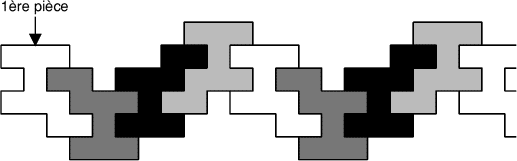
Lorsqu'il aura fini de poser la 40ème forme, quel sera
le périmètre de la frise ainsi formée?
- 8 - Les anniversaires
(coefficient 8)
- Aujourd'hui, on fête mes douze ans, et c'est aussi l'anniversaire de
mon père (qui a moins de 50 ans), et également celui de mon grand-père. Pour
l'occasion, on a acheté un jeu de dix bougies représentant les dix chiffres
de 0 à 9. Sur mon gâteau, on a disposé la bougie en forme de 1 et celle en
forme de 2 pour faire 12. Sur le gâteau de mon père, on a placé deux autres
bougies, de même que sur celui de mon grand-père. Ce dernier, qui est
astucieux, me dit:
On pourra encore réaliser ce tour de force l'an
prochain et dans deux ans, et alors toutes les bougies auront servi au
moins une fois, mais dans trois ans, il sera nécessaire d'acheter un autre
jeu de bougies
.
Quel est l'âge actuel de mon grand-père?
- 9 - Le panier de la ménagère
(coefficient 9)
- Remplissez les dix ronds de ce panier avec les nombres
de 0 à 9, en respectant les conditions suivantes:
- deux nombres directement reliés par un trait doivent avoir une
différence au moins égale à 3
- a > b
- c + d = 10.
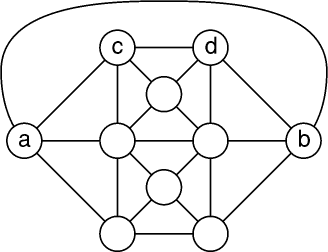
Note: l'anse du panier est considérée comme un trait.
Fin catégorie C1
- 10 - À livre ouvert
(coefficient 10)
- Durant leur dernier cours de math, Xavier et Yohann ont ouvert leur
livre au hasard, et ont chacun de leur côté effectué le produit des deux
numéros de pages visibles sur leur propre manuel. Quelle ne fut pas leur
surprise en comparant leurs résultats: la différence entre les deux était
exactement de 2000.
Quel est le plus grand numéro de page visible sur les deux livres
ouverts?
note: toutes les pages de gauche sont numérotées à l'aide d'un
nombre pair.
- 11 - Le trapèze du trappeur
(coefficient 11)
- Un lointain cousin, trappeur au Canada, vient de mourir. Dans
son testament, il me lègue une parcelle de terrain dont les quatre
côtés mesurent 150 m,
74 m,
175 m et
51 m. Le notaire, dans sa lettre,
me précise que les deux plus grands côtés sont parallèles et que
le prix actuel du terrain est de 45 dollars canadiens le
m². Quel est le prix de la
parcelle?
Fin catégorie C2
- 12 - Les fourmis géomètres
(coefficient 12)
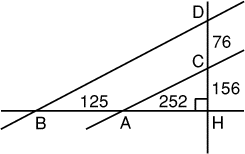
Deux fourmis se rencontrent au point H.
1ère fourmi: De B à A il y a 125 unités (de longueur fourmi),
et de A à H, il y en a 252
.
2ème fourmi: De D à C il y a 76 unités, et de C à H, il y en
a 156. De plus, (AB) est perpendiculaire à (CD).
1ère fourmi: (BD) et (AC) semblent parallèles.
2ème fourmi: Certainement pas, car l'entrée de ma
fourmilière se trouve à l'intersection de ces deux pistes!
1ère fourmi: Je me suis trompée, mais ta fourmilière doit
être bien loin...
Calculez la distance à vol d'oiseau de la fourmilière de la seconde
fourmi à la piste (AB). On donnera la réponse en unités-fourmi.- 13 - La pendule et les fourmis
(coefficient 13)
- Trois fourmis sont sur une pendule indiquant exactement quinze heures.
L'une dort au centre de la pendule; l'autre dort à l'extrémité de la petite
aiguille; quant à la troisième, située à l'extrémité de la grande aiguille
qui mesure 22 cm de long, elle vient
de se réveiller à 15 heures précises et a immédiatement pris la direction
du centre de la pendule en avançant à vitesse constante sur cette grande
aiguille de telle façon qu'elle met exactement une heure pour arriver au
centre de la pendule. Entre 15 et 16 heures, on a pu constater exactement
une fois que les trois fourmis formaient un triangle équilatéral.
Quelle est la longueur de la petite aiguille?
- 14 - Champolmat
(coefficient 14)
- Sur un vieux manuscrit, on a trouvé de curieuses opérations que
l'on peut transcrire comme ceci:
((1789  11)
11)  9) = 63
9) = 63
((2000 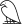 9)
9) 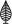 11) = 22
11) = 22
((((99 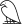 89)
89) 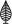 11)
11)
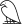 9)
9) 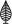 7) = 14
7) = 14
Le professeur Champolmat a découvert la clé de l'énigme que constituent ces
égalités. Le résultat de l'opération 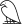 est le reste
dans la division euclidienne du premier nombre par le deuxième. Le résultat
de l'opération
est le reste
dans la division euclidienne du premier nombre par le deuxième. Le résultat
de l'opération 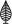 est le produit du premier nombre
par le deuxième. D'autre part, le signe d'égalité et les parenthèses jouent
le même rôle que pour nous aujourd'hui.
est le produit du premier nombre
par le deuxième. D'autre part, le signe d'égalité et les parenthèses jouent
le même rôle que pour nous aujourd'hui.
Champolmat découvre un peu plus tard un autre manuscrit avec une égalité
composée de nombres entiers établie à partir du même procédé.
Malheureusement, deux nombres, qui sont des entiers strictement positifs
(remplacés par x et y) sont illisibles.
((((((((((19 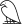 4)
4) 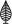 28)
28)
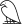 5)
5) 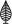 2)
2)
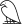 3)
3) 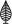 10)
10)
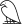 x)
x) 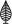 y)
y)
 13)
13)  4) = 16
4) = 16
Combien de nombres strictement inférieurs à 35 ne peuvent pas convenir
pour y? Donnez-en deux.
Fin catégories L1 GP
- 15 - La course infernale
(coefficient 15)
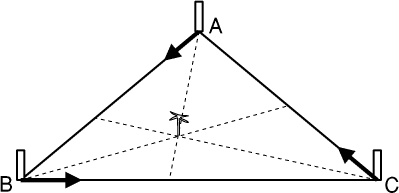
Les trois champions de course automobile Jean Alévazi, Mika Bekinen et
Mickael Choumaker se sont lancé un défi sur le pourtour du Grand Désert
Triangulaire, désert parfaitement plat, situé entre les villes d'Akilfécho,
de Brulissimo et de Célenferre. À 8 heures précises, Jean part d'Akilfécho,
Mika de Brulissimo et Mickael de Célenferre, chacun dans le sens indiqué
par la flèche. À 8 h
7 min très exactement, aucun n'a encore
atteint la ville vers laquelle il se dirige, mais les trois coureurs
tournent simultanément la tête vers leur gauche, et tous trois constatent
instantanément l'alignement parfait de l'unique palmier de ce désert et
du minaret de la ville située à l'opposé de leur position.
Akilfécho et Brulissimo sont distantes de
37,5 km, Brulissimo et Célenferre de
60 km, et Célenferre et Akilfécho de
42,75 km.
Lorsque les trois coureurs ont tourné la tête, ils avaient parcouru
exactement la même distance depuis leur départ. Quelle est cette
distance (on donnera la réponse arrondie au mètre le plus
proche)?- 16 - Au Lycée de l'Espace
(coefficient 16)
- Au Lycée de l'Espace, bien sûr, tous les élèves sont internes.
À leur arrivée, le Proviseur les accueille en leur disant qu'ils ne
pourront accéder à la fusée qui doit les ramener dans leurs foyers aux
prochaines vacances scolaires, qu'à l'aide d'un code ultra secret. Ce
code est la partie entière de la somme:
1/sqrt(1) + 1/sqrt(2) + 1/sqrt(3) + .......
+ 1/sqrt(1 003 002).
Quel est le code d'accès à la fusée?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org








 11)
11)  9) = 63
9) = 63