13^e Championnat International des Jeux Mathématiques et Logiques
demi-finale, 13 mars 1999

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Interdit de doubler (coefficient 1)

Gilles roule sur la Nationale 4, de Paris à Strasbourg, en passant par Nancy. Un panneau indique alors Nancy à 150 km et Strasbourg à 300 km. Tiens, c'est le double!, se dit-il.
Un peu plus tard, avant d'arriver à Nancy, Gilles constate qu'il n'est plus qu'à 50 km de Nancy.
À quelle distance de Strasbourg se trouve-t-il alors?

2 - La carte devinée (coefficient 2)

Un magicien doit deviner une carte. Une personne du public tire une carte dans un jeu (ordinaire) de 32 cartes, et la regarde sans la montrer au magicien. Voici le dialogue entre le magicien (M) et cette personne (P):
M: La carte est-elle un numéro?
P: Oui
M: Est-elle paire?
P: Oui
M: Est-elle un huit?
P: Non
M: La carte est-elle noire?
P: Oui
M: Est-elle un trèfle?
P: Non
Le magicien a déjà trouvé. Et vous?
Quelle était la carte tirée?
note: Un jeu ordinaire de 32 cartes comporte 4 couleurs: coeur (rouge), carreau (rouge), trèfle (noir), pique (noir), et, dans chaque couleur, 8 hauteurs: 7, 8, 9, 10, Valet, Dame, Roi, As.

Début catégorie C1

3 - Une nappe bien pliée (coefficient 3)

Une grande nappe carrée, 100% coton, est pliée, après repassage: une première fois en deux rectangles superposés, puis une 2^ème fois pour retrouver un carré plus petit, et encore, de la même façon, une 3^ème et une 4^ème fois.
Ce pliage terminé, la nappe est réduite à un carré de 24 cm de côté. Quel est le périmètre de cette nappe, entièrement dépliée, exprimé en centimètres?

4 - Le distributeur (coefficient 4)

Mathilde veut s'acheter une confiserie à 1 franc au distributeur de l'école. Celui-ci accepte les pièces en usage entre 5 centimes et un franc (5 c, 10 c, 20 c, 50 c, 1 F), mais il ne rend pas la monnaie. Mathilde n'a aucune pièce d'une valeur inférieure à 5 centimes, et aucune pièce ou billet d'une valeur supérieure à 1 franc. Elle possède cependant plus d'un franc dans son porte-monnaie, et pourtant, elle ne peut acheter sa confiserie, car elle est dans l'impossibilité de payer exactement 1 franc.
Combien Mathilde possède-t-elle, au maximum?

Début catégories C2 L1 L2 GP HC

5 - Entre chats et chien (coefficient 5)

Mathias doit deviner le nom d'un animal (en cinq lettres).

C H A T S   0 | 2
L I O N S   1 | 0
T I G R E   2 | 0
P A O N S   0 | 0
B O E U F   1 | 1
C H I E N   0 | 4
---------
_ _ _ _ _

Il a proposé à Mathilde les noms d'animaux ci-contre, et, à chaque fois, elle lui a répondu en donnant, dans cet ordre, le nombre de lettres justes et bien placées, et le nombre de lettres justes mais mal placées. Ainsi, pour CHATS, il n'y a aucune lettre juste et bien placée, et il y a deux lettres justes mais mal placées.
Quel est le nom de l'animal à deviner?

6 - Une histoire à tourner en rond (coefficient 6)

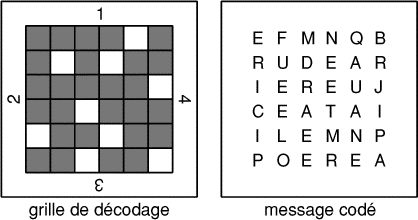
Alice a envoyé un message codé à Bob. Malheureusement, celui-ci a laissé traîner le message et la grille de décodage. Charles, qui passait par là, a su trouver la signification du message.
Quelle phrase Alice a-t-elle envoyée?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - La famille Septime (coefficient 7)

Monsieur et Madame Septime ont sept enfants nés, curieusement, tous les sept un 7 juillet. Chaque année, pour leur anniversaire, Madame Septime offre à chacun un gâteau comportant autant de bougies qu'il a d'années. Jean Septime, le plus jeune, se souvient qu'il y a cinq ans, il y avait, au total, deux fois moins de bougies que cette année.
Combien de bougies seront allumées cette année?

8 - Le poids des ans (coefficient 8)

Le village de Cent-le-Vieux compte exactement 100 habitants. Le plus âgé est né en 1900 et tous les habitants sont nés une année différente, mais tous le 1^er janvier.
En 1999, la somme des quatre chiffres de l'année de naissance de Jules est égale à son âge. Quel est l'âge de Jules?

9 - Dialogue de sous (coefficient 9)

Tic et Tac ont fait de gros progrès en arithmétique et ils s'affrontent maintenant en ces termes:
Tic: Le montant de mes économies est très supérieur au tien! C'est un nombre à 3 chiffres, c'est un multiple de 9 et il se termine par un 8.
Tac: Celui des miennes est aussi un nombre à trois chiffres. Mais c'est seulement un multiple de 3 et il se termine par un 2!
Combien de francs Tic possède-t-il de plus que Tac, au maximum?

Fin catégorie C1

10 - Le livre de Mathilde (coefficient 10)

Mathilde lit un livre de 225 pages. La somme des chiffres des numéros des deux premières pages du deuxième chapitre est égale à 18. Chose curieuse, la somme des chiffres des numéros des deux dernières pages de ce chapitre est aussi égale à 18. Ce chapitre compte plus de 2 pages.
Combien de pages le deuxième chapitre du livre de Mathilde compte-t-il?

11 - Le terrain d'Yhieux (coefficient 11)

Le père Yhieux, qui n'a jamais eu froid aux yeux, possède un terrain rectangulaire presque carré: sa longueur et sa largeur, qui sont des nombres entiers de mètres, diffèrent d'exactement un mètre. L'aire du terrain du Père Yhieux, exprimée en mètres carrés, est un nombre remarquable à 4 chiffres: son chiffre des mille et son chiffre des centaines sont égaux, et il en est de même de ses chiffres des dizaines et des unités.
Quelle est la largeur du terrain d'Yhieux?

Fin catégorie C2

12 - Carrés très spéciaux (coefficient 12)

Le plus petit entier dont la somme des chiffres vaut 1 est le nombre 1. Le plus petit entier dont la somme des chiffres vaut 2 est le nombre 2. Le plus petit entier dont la somme des chiffres vaut 3 est le nombre 3... Le plus petit entier dont la somme des chiffres vaut 10 est le nombre 19. Le plus petit entier dont la somme des chiffres vaut 11 est le nombre 29. etc.
On écrit ainsi la liste de nombres obtenue (elle est infinie): 1, 2, 3, ......, 19, 29, .....
Quel est le plus grand nombre de cette liste qui soit le carré d'un nombre entier?
Répondez 0 si vous pensez qu'un tel nombre n'existe pas.

13 - L'aquarium (coefficient 13)

Un aquarium posé sur une table a la forme d'un parallélépipède rectangle de hauteur 30 cm. On le remplit d'eau à ras bord, puis on le fait pivoter autour d'une des arêtes de la base, jusqu'à ce que le fond fasse un angle de 45° avec le plan de la table. Un tiers de son contenu se répand alors sur la table.
On le remplit à nouveau à ras bord, puis on le fait pivoter autour d'une autre arête de la base, jusqu'à ce que le fond fasse à nouveau un angle de 45° avec le plan de la table. Les quatre cinquièmes de son contenu se répandent alors sur la table.
Quel est le volume de l'aquarium (on donnera la réponse en cm³)?

14 - Un partage du carré (coefficient 14)

On partage un carré en huit triangles rectangles tous différents les uns des autres, mais aussi tous semblables: la longueur du plus grand côté de l'angle droit est toujours égale au double de celle du petit. La figure ci-contre, qui ne respecte pas les proportions, montre le résultat obtenu.

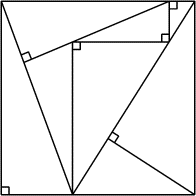
Toutes les surfaces des triangles, exprimées en cm², sont des nombres entiers.
Quelle est, au minimum, l'aire du carré, exprimée en cm²?

Fin catégories L1 GP

15 - La polka des disques (coefficient 15)

Deux disques A de centre O et B de centre P, tangents extérieurement, pratiquent le mouvement de danse suivant, qui comprend deux temps. A commence par rouler sur B, dans le sens des aiguilles d'une montre, de façon que son centre ait tourné d'un angle α strictement compris entre 0° et 180° autour du point P. Ensuite, c'est au tour de B de rouler autour de A, dans le sens des aiguilles d'une montre, d'un angle α/2 autour du point O.
Les partenaires effectuent 10 mouvements complets de cette danse, après quoi ils se retrouvent pour la première fois globalement dans leur position de départ.
Donnez la valeur de l'angle α en degrés.

16 - Choix sur l'échiquier (coefficient 16)

Sur un échiquier 11 × 11, on a choisi 22 cases à raison de deux par ligne et deux par colonne (un exemple est donné ci-contre). Deux choix sont considérés comme équivalents s'ils peuvent se déduire l'un de l'autre par des permutations de lignes et des permutations de colonnes. Combien existe-t-il de choix non-équivalents?

Fin catégories L2 HC