11e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels
Date limite: 15 janvier 1997. Vous pouvez trouver les énoncés des problèmes, un bulletin-réponse et toutes les autres infos sur le championnat dans le numéro 53 du magazine Tangente.
Catégories
Énoncés des problèmes
Début catégorie CM
- 1 - Les deux fourmis
(coefficient 1)
- Deux fourmis se trouvent sur un cube en fil de fer. La fourmi B
est immobile. La fourmi A désire rejoindre la fourmi B.
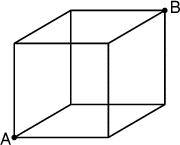
Si l'on prend la longueur d'une arête pour unité de longueur, le chemin le
plus court a pour longueur 3.
Combien de chemins différents de longueur 3 la fourmi A peut-elle
emprunter pour rejoindre la fourmi B?
- 2 - Il y a plus d'un âne qui s'appelle Martin
(coefficient 2)
- Les trois ânes Martin1, Martin2 et Martin3 vont à la foire, et ils
attendent d'être chargés. Il y a neuf colis pesant respectivement 1, 2, 3,
4, 5, 6, 7, 8, 9 kg. Chacun des trois ânes
reçoit le même nombre de colis et la même charge que les autres. De plus,
Martin1 doit porter le paquet de 1 kg, Martin2 doit porter le paquet
de 2 kg, et Martin3 doit porter le paquet de 3 kg.
Comment peut-on répartir le chargement entre les trois ânes?
Début catégorie C1
- 3 - Les trois amis
(coefficient 3)
- Trois amis habitent trois maisons voisines de la même rue,
aux numéros 34, 36, 38. Leurs couleurs de cheveux sont différentes
et leurs loisirs préférés diffèrent également.
Le brun fait de la plongée sous-marine.
La maison dont le numéro se divise par 4 est habitée par le blond. Le
footballeur est content d'habiter une maison dont le numéro a pour somme
de ses chiffres le nombre de joueurs d'une équipe professionnelle de son
sport favori.
Quel est le numéro de la maison du musicien?
note: une équipe professionnelle de football compte onze joueurs.
- 4 - Les fourmis déménagent
(coefficient 4)
- Deux familles de cinq fourmis chacune, les unes rouges, les autres
noires, ont décidé d'échanger leurs résidences d'été. Chaque fourmi
emporte son bagage sur son dos et met trois minutes trente secondes
pour rejoindre le domicile visé.
Le voyage se déroule ainsi: le départ des premières fourmis se situe au
même moment pour les deux familles, et ensuite chaque fourmi part seule
une minute après la précédente. Comme il n'y a qu'une route entre les deux
nids, il y a des croisements entre rouges
et noires
et, à
cette occasion, chaque fourmi souhaite bonnes vacances
à l'autre.
Mais curieusement, chez les fourmis, il n'y a pas de formule de politesse
à l'intérieur des maisons.
Combien de souhaits seront prononcés pendant le déménagement?
Début catégories C2 L1 GP L2 HC
- 5 - Points de vue symétriques
(coefficient 5)

Les cinq cubes alignés sont tous identiques.
De ce côté, vous pouvez lire 06129.
Que liriez-vous si vous étiez situé de l'autre côté du mur de
cubes?- 6 - Le jeu de Lam
(coefficient 6)
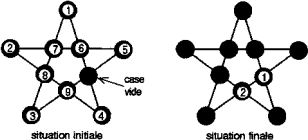
Je n'y arrive pas, se lamentait la Martine.
C'est le grand Lama en personne qui m'a appris ce jeu au Tibet: les
pions sautent en suivant les lignes tracées par dessus un autre
pion jusqu'à une case vide. Le pion sauté est alors éliminé. À la fin,
il ne doit plus rester que les pions 1 et 2 disposés comme sur la
figure.
Bernard, fine lame en casse-tête, cessa de dessiner un lamentin, prit en
main le pion n°3, et tenta sa chance...
Sept coups plus tard, il vint à bout du problème du grand Lama!
Fais aussi bien que Bernard, en débutant comme lui. Tu noteras ta
solution en indiquant à chaque coup le numéro du pion sauteur et celui
du pion éliminé (le premier coup, par exemple, sera noté 3-9).
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - La montre de Jules
(coefficient 7)
- La belle Cléo a reçu de son ami Jules une magnifique montre
à affichage digital en chiffres romains. Cette montre affiche les
heures et les minutes, séparées par un tiret. À 6 heures 29,
par exemple, elle affiche VI-XXIX, et à
6 h 04, VI-IV.
On dit que ce dernier affichage est palindrome, car on le lirait
de la même façon de droite à gauche que de gauche à droite.
De 0 h 01 à
23 h 59, combien de fois
aura-t-on un affichage palindrome?
notes: on tiendra compte de la position du tiret; on rappelle que le
chiffre zéro n'existe pas dans l'écriture en chiffres romains; pour
les nombres de 1 à 23, on n'utilise que l'écriture suivante: I, II,
III, IV, V, VI, VII, VIII, IX, X, XI, XII, XIII, XIV, XV, XVI, XVII,
XVIII, XIX, XX, XXI, XXII, XXIII.
- 8 - Rendez-vous à Carréville
(coefficient 8)
- Carréville est entièrement constituée de pâtés de maisons carrés de
50 mètres de côté, entourés de rues formant un quadrillage régulier.
Juliette et Roméo ne s'y déplacent qu'en vélo.

Aujourd'hui, Juliette a donné rendez-vous à Roméo en un carrefour situé à
égale distance (en vélo, et non à vol d'oiseau) du Carrefour des Bateliers
(B) et de celui des Camionneurs (C). Mais ce carrefour est situé également
à égale distance (toujours en vélo) du Carrefour des Aviateurs (A) et de
celui des Déménageurs (D).
Roméo hésite entre deux carrefours.
Quels sont ces deux carrefours?
Vous les indiquerez par une croix sur le bulletin-réponse.
- 9 - Les 7 nombres
(coefficient 9)
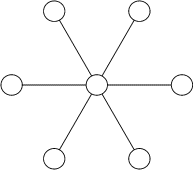
Vous complétez les 7 disques du dessin ci-contre à l'aide de 7 entiers
plus grands que 0 et tous différents, de telle sorte que la somme des
nombres portés par deux disques directement reliés par un segment ne
soit jamais divisible ni par 2, ni par 3.
Quelle est la plus petite valeur possible de la somme des
7 nombres?
Fin catégorie C1
- 10 - Puzzle coloré
(coefficient 10)

Avec ces pièces (quatre carrés de dimensions 2 sur 2 et huit rectangles
de dimensions 3 sur 1) coloriées comme sur le dessin (B pour bleu, J
pour jaune, V pour vert et R pour rouge), on doit remplir une boîte
rectangulaire de dimensions 5 sur 8.
Règle de rangement: deux pièces de même couleur ne doivent en aucun cas
se toucher, même par un sommet. Il en est de même pour deux carrés.

Le puzzle a déjà été commencé (voir croquis) en disposant un carré bleu,
un rectangle rouge et un rectangle jaune.
Terminez le rangement de toutes les pièces dans la boîte.
N.d.V.L.: le nombre de solutions n'est pas demandé; il faut juste
donner deux solutions.- 11 - Transcoloriages
(coefficient 11)
- On dispose de 64 petits cubes de même taille numérotés de 1
à 64.
On les range de la manière suivante pour constituer un grand cube.
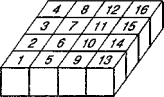
La seconde tranche est constituée de la même façon en commençant par le
cube 17 placé au-dessus du 1, le cube 18 placé au-dessus du 2, etc.
Ordonnée de la même façon, la troisième tranche débute par le numéro 33,
la quatrième par le numéro 49, etc.
Une fois le grand cube constitué, on le peint extérieurement en vert,
sur ses six faces, puis on le démonte dès qu'il est sec.
On utilise alors les petits cubes pour reconstituer un grand cube de la
manière suivante:
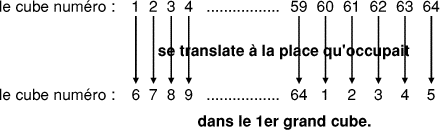
Chaque déplacement se faisant par une translation, les orientations de
cubes sont conservées.
Ce deuxième grand cube étant constitué, on le peint extérieurement en
rouge, sur ses six faces.
Après ce deuxième coloriage, combien de petits cubes comportent
exactement deux faces colorées, l'une en vert, et l'autre en rouge?
Donnez deux de ces cubes, par leur numéro.
Fin catégorie C2
- 12 - Douze nombres pour une étoile
(coefficient 12)
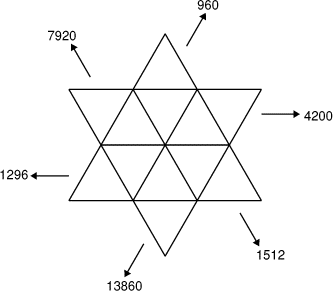
Les nombres entiers de 1 à 12 ont été placés dans chacune des cases
de l'étoile ci-contre.
Les nombres écrits à l'extérieur représentent les produits des cinq
nombres placés à l'intérieur de l'étoile et situés dans la direction
de la flèche.
Retrouvez la place des nombres de 1 à 12.- 13 - Si la distance m'était comptée
(coefficient 13)
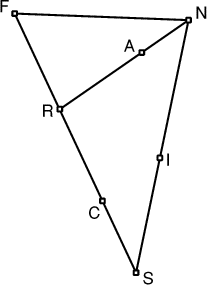
Les villes F, R, A, N, C, I et S sont disposées comme sur le dessin
ci-contre. On sait, de plus, que
FR = RA = RI = RC = 24 km,
et
NF = NI = NR = 40 km.
Quelle distance sépare les deux villes S et I?
(les proportions du dessin ne sont pas exactes).- 14 - Effets de lumière
(coefficient 14)
- Christophe a fabriqué un commutateur à trois touches pour commander
les effets lumineux lors d'une soirée dansante.
Celui-ci commande 100 ampoules numérotées par les entiers positifs de
1 à 100, toutes en état de fonctionner.
En appuyant sur la première touche du commutateur, on change l'état de
toutes les ampoules: celles qui étaient allumées s'éteignent, et celles
qui étaient éteintes s'allument.
En appuyant sur le second bouton, on change l'état des ampoules portant
un numéro impair.
En appuyant sur le troisième bouton, on change l'état de toutes les
ampoules portant un numéro qui est un multiple de 3 augmenté de 1.
En début de soirée, toutes les ampoules étaient allumées. Au cours de
la soirée, Christophe a appuyé 1000 fois, de façon aléatoire, sur les
touches de son commutateur. Lorsqu'il a appuyé pour la dernière fois
sur une des touches, il a remarqué que les ampoules portant les numéros
95 et 96 étaient éteintes.
Combien d'ampoules étaient alors allumées?
Fin catégories L1 GP
- 15 - Le rayon dans la boîte
(coefficient 15)
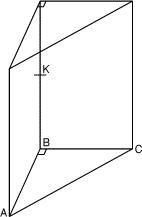
Les parois intérieures d'une boîte en forme de prisme droit
(voir figure) ont été habillées de miroirs. La base ABC est
un triangle isocèle rectangle en B, tel que
AB = 1 m. D'un point K
situé sur une arête verticale, on émet un rayon lumineux orthogonal à
cette arête, qui se reflète plusieurs fois sur les parois latérales du
prisme avant de toucher à nouveau une arête.
Sachant que le rayon lumineux a parcouru 13 mètres, combien de fois
s'est-il réfléchi?- 16 - Cube pluridivisible
(coefficient 16)
- Le cube d'un nombre entier positif a cinq fois plus de diviseurs
que ce nombre entier positif.
Combien de diviseurs possède le carré du nombre de départ?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org











