11^e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 24 mai 1997

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Le gâteau de José (coefficient 1)

José a invité Mathias et Mathilde, et il leur propose un gâteau numérique, constitué de neuf petits carrés portant chacun un chiffre en fruits confits, comme sur le dessin représenté ci-contre. José demande à ses amis de partager ce gâteau en trois morceaux contenant chacun un nombre entier de carrés. De plus, si on totalise les chiffres écrits sur les carrés de chaque part, on doit obtenir le même total. Mathilde a commencé le partage par le trait indiqué par la flèche.

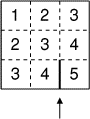
Terminez le partage du gâteau.

2 - La noix de son maître (coefficient 2)

Gaston Lenôtre a devant lui un grand tas de noix que son chien Médor lui a apporté (entre 1 et 97 noix). Il partage le tas en deux nouveaux tas égaux; s'il reste une noix, il la donne au chien, puis met de côté l'un des 2 tas. Il recommence avec le tas restant, en donnant à chaque fois la noix qui reste, s'il en reste une, ainsi que la dernière noix.
Combien Médor a-t-il mangé de noix, au maximum?

Début catégorie C1

3 - Le 98^ème de la liste (coefficient 3)

On écrit un nombre ayant un chiffre avant la virgule et un chiffre après la virgule, par exemple 4,1 (1^er nombre de la liste). On échange alors la partie entière et la partie décimale de ce nombre (4,1 donne 1,4), puis on calcule la différence entre les deux nombres (le plus grand moins le plus petit: 4,1 - 1,4), et on écrit le résultat: 2,7 (2^ème nombre de la liste). On peut alors recommencer avec 2,7 (2,7 donne 7,2, et 7,2 - 2,7 = 4,5)...
Si le premier nombre écrit est 9,7 et qu'on applique le même procédé 97 fois, quel sera le dernier nombre écrit, c'est-à-dire le 98^ème?

4 - Problème de voisinage (coefficient 4)

Dans les cercles du dessin ci-dessous, inscrivez les chiffres de 1 à 9 de telle sorte que:

• le chiffre 2 soit écrit immédiatement à droite de 8 et juste au-dessous de 4,
• le chiffre 6 soit écrit immédiatement à droite de 3 et immédiatement à gauche de 9,
• le chiffre 7 soit écrit immédiatement à gauche de 1 et juste au-dessus de 5.

Début catégories C2 L1 L2 GP HC

5 - De ZERO à SIX (coefficient 5)

On considère les nombres dont l'écriture en lettres (en français) comporte au plus 4 lettres (par exemple: UN, HUIT, ...). On peut passer d'un nombre à un autre si leurs écritures en lettres comprennent au moins deux lettres communes (exemple: CENT ---> NEUF ---> UN ...). On veut passer de ZERO à SIX:
ZERO ---> ..................................... --> SIX
Combien de nombres écrira-t-on, au minimum, ZERO et SIX compris? Répondez 0 si vous pensez que c'est impossible.

6 - La longueur du DÉFI (coefficient 6)

Un terrain rectangulaire DEFI est partagé en six parcelles de même forme et de même aire. Sur le plan ci-contre, la disposition des parcelles est respectée, mais les distances et les proportions ne sont pas justes.

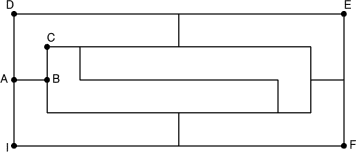
On sait seulement que AB = BC = 1 hm.
Quelle est la longueur du rectangle DEFI, exprimée en hectomètres?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Les pions sur l'échiquier (coefficient 7)

On veut poser 31 pions sur l'échiquier de 49 cases représenté ci-contre de telle sorte que ces 31 pions forment un ensemble symétrique par rapport à chacune des deux diagonales de l'échiquier.
Combien de pions, au minimum, seront posés sur les cases des diagonales (représentées en grisé)?

8 - Opérations de l'année (coefficient 8)

En utilisant cinq nombres différents pris parmi 1000, 9, 100, 4, 20, 10, 7, et en utilisant dans cet ordre les 4 opérations ÷ × + -, obtenez 1997.

9 - Le terrain bis-Cornu (coefficient 9)

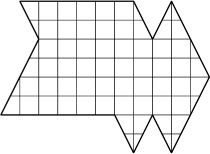
Monsieur Cornu est propriétaire de deux terrains. Il décide de donner son second terrain, représenté ci-contre à ses quatre enfants. Mais il exige que les quatre parcelles aient la même forme et la même aire.
Faites le découpage du terrain.

Fin catégorie C1

10 - Course contre la montre (coefficient 10)

Tony, Michel et Jean-François tentent de battre un record à vélo, sur un parcours en équipe de 100 km.
Comme il s'agit de collaborer efficacement, ils décident de prendre des relais (c'est-à-dire de rouler en tête pour protéger les coéquipiers du vent) d'une façon originale mais régulière: deux d'entre eux prendront des relais de 2 kilomètres, et le plus vigoureux prendra un relais d'un kilomètre seulement, mais plus tonique, les relais se faisant dans le même ordre tout au long de la course.
On sait que Tony était en tête pendant le 72^ème km, que Jean-François menait la course pendant le 89^ème km, et que Michel emmenait le groupe pendant le 93^ème km.
Pouvez-vous dire dans quel ordre les trois hommes ont choisi de se relayer au début de la course?

11 - L'emprunt raté (coefficient 11)

Charles dit à Gaston: Prête-moi 72 francs.
Je ne peux pas te prêter cette somme, car je n'ai pas autant sur moi, répond Gaston. Si j'avais deux fois la somme que j'ai, alors j'aurais, en plus de ce que tu me demandes, la somme qu'il me manque pour pouvoir te prêter 72 F.
De quelle somme dispose Gaston?

Fin catégorie C2

12 - Les trois footballeurs (coefficient 12)

Trois amis ont acheté ensemble un ballon de foot pour 450 F, qu'ils ont payé à eux trois.
Le premier a déboursé une somme inférieure ou égale à celle payée par ses deux amis ensemble. Le deuxième a déboursé une somme inférieure ou égale à la moitié de celle payée par ses deux amis ensemble. Quant au troisième, il a déboursé une somme inférieure ou égale au cinquième de celle payée par ses deux amis ensemble.
Combien chacun a-t-il payé?

13 - Les nombres glissants (coefficient 13)

Le nombre 20 est un nombre glissant, car 20 = 10 + 10, et 1/10 + 1/10 = 0,20, qui s'écrit comme le nombre 20, simplement précédé d'un 0 et d'une virgule.
Un nombre glissant est un nombre qui peut se décomposer en une somme de deux entiers a et b, pas nécessairement égaux, tels que la somme des inverses de a et de b s'écrive (en base 10) avec les chiffres du nombre de départ, écrits dans le même ordre, et précédés de 0 et d'une virgule.
Combien y a-t-il d'autres nombres glissants à deux chiffres? Trouvez-en deux.

14 - Le partage d'Eugène (coefficient 14)

Le grand architecte Eugène Iteur adorait les nombres entiers. Admirateur de Pythagore et de Thalès, il acheta sur ses vieux jours, dans la région du Puy de Dôme (département 63), un terrain triangulaire ABC dont les dimensions en mètres étaient, malicieusement, AB = 13 √63, AC = 15 √63 et BC = 14 √63.

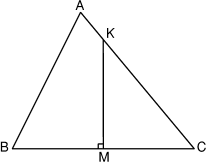
Quand il mourut, ses deux fils, Délim et Facil, eurent à se partager le terrain, les deux parts devant avoir la même aire.

• Délim souhaita un mur de séparation rectiligne entre les deux parties.
• Facil dit qu'il n'y avait qu'à construire ce mur perpendiculairement au côté BC.

Quelle est en mètres, éventuellement arrondie au centimètre, la longueur du mur de séparation?
On pourra prendre 2,646 pour √7.

Fin catégories L1 GP

15 - La boule de Chris Thal (coefficient 15)

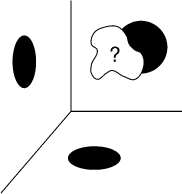
Pour prédire l'avenir, Christine Thal, dite Chris, voyante de son état, utilise une bien curieuse boule de cristal qu'elle nous décrit de la manière suivante:
Quand Elle est éclairée du dessus, son ombre projetée sur un plan horizontal situé en-dessous est un disque circulaire plein.
Quand Elle est éclairée par la droite, son ombre projetée sur un plan vertical situé à gauche est un disque circulaire plein identique au premier.
Quand Elle est éclairée par l'avant, son ombre projetée sur un plan vertical situé derrière est un disque circulaire plein identique aux deux autres.
De plus, de tous les objets ayant ces caractéristiques, c'est celui qui a le plus grand volume.
Combien la boule de Chris Thal comporte-t-elle de faces (pas nécessairement planes)?

16 - L'héritage de Circulus (coefficient 16)

Circulus, l'empereur romain bien connu, veut partager sa somptueuse propriété entre ses 4 enfants, 3 fils et une fille. Cette propriété a la forme d'un triangle équilatéral de 8 kilomètres de côté. De chaque sommet de ce triangle part une route rectiligne qui joint le côté opposé. La part de chaque fils a la forme d'un triangle dont un côté coïncide avec un côté de la propriété, chacun des autres côtés étant longé par une route. La part de la fille a la forme d'un triangle dont chaque côté est longé par une route (sur la figure, les pointillés indiquent la prolongation des routes).
Circulus veut que chacun de ses enfants puisse aménager une arène circulaire à l'intérieur de sa part. Ces arènes, destinées aux jeux, ont toutes le même rayon.

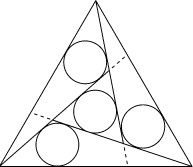
Quel est ce rayon, au maximum? On donnera ce rayon arrondi au mètre le plus proche. Si besoin est, on pourra prendre 1,414 pour √2; 1,732 pour √3; 2,236 pour √5; 2,646 pour √7.

Fin catégories L2 HC