11^e Championnat International des Jeux Mathématiques et Logiques
demi-finale, 15 mars 1997

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Cent carrés? (coefficient 1)

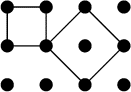
En comptant les deux carrés déjà tracés, combien peut-on dessiner de carrés, au maximum, ayant leurs sommets pris parmi les douze points du dessin ci-contre?

2 - La petite pyramide (coefficient 2)

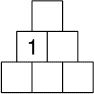
Compléter la pyramide ci-contre avec les nombres de 2 à 6 de telle sorte que, excepté pour la rangée du bas, un nombre soit toujours égal à la différence des deux nombres situés juste au-dessous.

Début catégorie C1

3 - Le collectionneur (coefficient 3)

Tom collectionne les papillons. Il garde ses spécimens dans onze boîtes. Chacune des onze boîtes contient au moins un papillon. Huit de ces onze boîtes en contiennent chacune au moins deux, six en contiennent chacune au moins quatre et deux boîtes en contiennent exactement cinq chacune.
Combien la collection de Tom compte-t-elle de papillons, au minimum?

4 - La cueillette des champignons (coefficient 4)

Anatole, Béatrice, Chantal et Damien sont allés ramasser des champignons et sont rentrés avec leurs paniers remplis de cèpes.
Damien en avait plus que Chantal, mais Anatole en avait moins que Chantal.
Enfin, Anatole et Béatrice en avaient ensemble autant que Chantal et Damien réunis.
Qui en avait le plus? Qui en avait le moins?

Début catégories C2 L1 L2 GP HC

5 - Le terrain du père Cutant (coefficient 5)

Le père Cutant, Xavier-Édouard, possède un terrain ayant la forme représentée ci-après. Quatre magnifiques chênes sont plantés sur ce terrain. Le père Cutant décide de partager son terrain, pour ses 4 enfants, en 4 parcelles de même forme et de même aire, chaque parcelle devant contenir un des chênes.

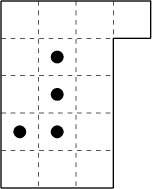
Aidez X.-É. Cutant à faire le partage, en dessinant sur le plan le contour des quatre parcelles.

6 - Le nombre à 7 chiffres (coefficient 6)

Dans ce nombre à sept chiffres formé des chiffres 1, 2, 3, 4, 5, 6 et 7 pris chacun une fois, la somme de deux chiffres successifs est toujours égale soit à la somme des deux premiers chiffres, soit à la somme des deux derniers. Trouvez ce nombre.
On demande une seule solution.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le petit quotient (coefficient 7)

On divise un nombre à deux chiffres par la somme de ses chiffres.
Exemple: 23 : (2+3) = 23 : 5 = 4,6
Quel est le plus petit quotient que l'on puisse obtenir?
Si besoin est, on arrondira au millième.

8 - Le carré latin (coefficient 8)

Dans un tableau carré de 5 cases sur 5 cases, on inscrit les nombres 1, 2, 3, 4, 5, de telle sorte que:

• sur chaque ligne et sur chaque colonne apparaissent chacun des 5 nombres
• le tableau rempli est symétrique par rapport à une de ses deux diagonales.

Quelles sont la valeur minimum et la valeur maximum de la somme des 9 nombres écrits dans les deux diagonales du tableau?

9 - C'est pas de la tarte! (coefficient 9)

C'est l'anniversaire de Mathilde. Ses deux amis Mathias et José lui ont apporté une superbe tarte carrée. D'un coup de couteau magistral et rectiligne, Mathias coupe le gâteau en deux morceaux, puis, d'un second coup lui aussi rectiligne, il partage l'un des morceaux en deux, ce qui donne finalement trois belles parts, la plus grosse étant évidemment destinée à Mathilde.
Mathilde prend alors son rapporteur (lavable) et mesure tous les angles des trois parts. Elle additionne ensuite toutes ces mesures à l'aide de sa supercalculatrice (résistante à l'eau et au yaourt).
Combien trouve-t-elle, au minimum?
On donnera la réponse en degrés.

Fin catégorie C1

10 - Les deux soeurs (coefficient 10)

Les deux soeurs, Barbara et Monique, fêtent aujourd'hui leur anniversaire commun, puisqu'elles sont nées le même jour du même mois, Barbara étant plus jeune de 2 ans. À une question sur son âge, Monique répond:
Barbara est très jeune, puisqu'elle compte moins d'années que nous n'en avions ensemble il y a neuf ans. Quant à moi, je suis vieille, puisque je compte plus d'années que nous n'en avions ensemble il y a neuf ans.
Quel âge a Barbara?

11 - Le grand chambardement (coefficient 11)

Dans une suite numérique, on a le droit d'effectuer l'opération suivante:
on choisit plusieurs termes qui se suivent (au minimum 2 termes, au maximum, la suite entière), et on renverse l'ordre de ces termes, le reste éventuel de la suite demeurant inchangé.

                  ----------
Exemple: 8, 1, 6, 2, 3, 9, 4, 7
donne    8, 1, 6, 4, 9, 3, 2, 7.

En combien d'opérations, au minimum, pourra-t-on passer de la suite 8, 9, 3, 4, 5, 6, 7, 1, 2, à la suite 1, 2, 3, 4, 5, 6, 7, 8, 9?

Fin catégorie C2

12 - Jeu du cavalier (coefficient 12)

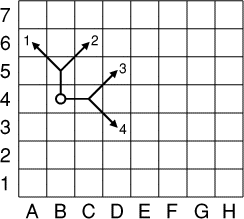
Un cavalier d'échecs se trouve initialement sur la case B4 d'un échiquier de 8 cases sur 7 cases. Étant sur une case quelconque, il peut effectuer l'un des quatre mouvements indiqués sur la figure (à condition qu'il soit réalisable sans sortir de l'échiquier), et seulement l'un de ces quatre là.
Les deux joueurs déplacent le cavalier à tour de rôle jusqu'à ce qu'un joueur ne puisse plus jouer. Le dernier joueur ayant pu jouer est alors déclaré vainqueur.
Vous jouez le premier. Cochez sur le bulletin-réponse la ou les cases correspondant à votre premier mouvement si vous voulez être sûr de gagner, quel que soit le jeu de votre adversaire (chaque mouvement est désigné par son numéro sur la figure ci-dessus).
Répondez 0 solution si vous pensez que le second joueur sera gagnant quel que soit votre jeu.

13 - Maxi-fléchettes (coefficient 13)

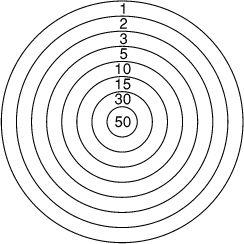
Après un tournoi de fléchettes âprement disputé, Adrien, Bernard, Cyril, Daniel, Émile et Francis se détachent du lot de tous les concurrents: ils sont ex-aequo.
Le jury décide une ultime épreuve pour les départager: chaque concurrent devra lancer ses six fléchettes d'une distance inhabituelle; le total des scores décidera du vainqueur.
Hélas, après tous les lancers, et bien que toutes les fléchettes eussent atteint la cible, que les candidats aient, à chaque lancer, réalisé un score au moins aussi bon qu'au lancer précédent, et que les listes de scores des six candidats soient toutes différentes, le jury constate avec stupeur que les six candidats ont tous réalisé un total de 97 points!
Si seuls les trois meilleurs scores étaient pris en compte, il y aurait encore trois premiers ex-aequo: Cyril, Daniel et Émile.
L'épreuve n'ayant que trop duré, le jury décide alors de classer les candidats d'après le produit des six scores réalisés, le produit le plus élevé donnant le gagnant.
Les résultats ayant été affichés, on put remarquer que:

• aucun candidat n'a obtenu trois fois le même score
• Bernard et Adrien auraient été ex-aequo si on avait additionné les quatre meilleurs scores
• Adrien n'a jamais atteint le 30
• Cyril a obtenu une fois le plus mauvais score possible
• Daniel, le perdant, a pourtant atteint le centre de la cible, alors que Francis, déclaré vainqueur, ne l'a pas atteint!

Donnez les produits des scores obtenus par les concurrents (en milliers).

14 - La suite périodique (coefficient 14)

Un ordinateur exécute le programme suivant:
Si l'on introduit deux chiffres a et b, il les écrit, puis il écrit le chiffre des unités de la somme a + b. Il continue ensuite en écrivant à chaque étape le chiffre des unités de la somme des deux termes précédents. José, après avoir introduit les deux premiers chiffres tels que a < b, constate que l'ordinateur obtient une suite de quatre chiffres qui se répète indéfiniment.
Quels étaient les deux chiffres introduits par José?

Fin catégories L1 GP

15 - Le jeu du polynôme (coefficient 15)

Un professeur propose à ses élèves de trouver la racine entière d'un polynôme P à coefficients entiers.
À tour de rôle, les élèves proposent un nombre a, et le professeur annonce la valeur de P(a) et la position de a par rapport à la racine entière.
_ Julien: 7.
_ Le professeur: P(7) = 77, et la racine est supérieure à 7.
_ Bernard: ...... (inaudible du reste de la classe, mais supérieur à 7).
_ Le professeur: P(...) = 85, et la racine est supérieure au nombre proposé.
Quelle est la valeur de la racine entière?

16 - Les deux dés (coefficient 16)

On dispose de deux dés cubiques portant sur leurs faces des nombres entiers de 1 à 12, pas nécessairement tous différents. On lance ces deux dés et on additionne les nombres de points qu'ils indiquent. On peut obtenir ainsi tous les nombres de 2 à 19 avec la même probabilité.
Quels nombres portent les faces des deux dés? Pour chaque dé, on donnera ces nombres par ordre croissant.

Fin catégories L2 HC