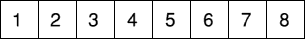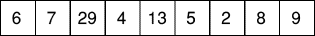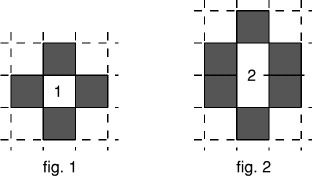10e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 11 mai 1996
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Quand nous jouions à la marelle
(coefficient 1)
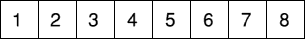
Aline joue à la marelle. Elle vient de sauter sur une case. La somme
des nombres marqués sur les cases situées à sa gauche est égale à la
somme des nombres marqués sur les cases situées à sa droite.
Sur quelle case se trouve-t-elle?- 2 - Les deux dés de Dédé
(coefficient 2)

Dédé Bonnaire possède deux dés, un blanc et un noir. Il vient de les
lancer tous les deux, plusieurs fois de suite. Chose remarquable, le
total des points figurant sur les deux faces du dessus était toujours
égal à 8, comme sur la figure, et pourtant le dé blanc n'a jamais
indiqué le même nombre de points.
Combien de fois, au maximum, D. Bonnaire a-t-il lancé ses deux
dés?
Début catégorie C1
- 3 - Les tartes de Pat Hissier
(coefficient 3)
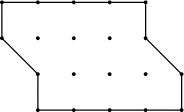
Pat Hissier fait des tartes ayant une forme très originale: celle
représentée sur la figure ci-dessus. Ses tartes sont prévues pour
quatre personnes.
Trouvez un découpage de la tarte de Pat en quatre parts parfaitement
superposables.- 4 - Éliminez
(coefficient 4)
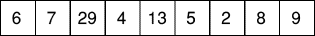
Dans la liste des nombres ci-dessus, éliminez deux nombres de somme 12 et
de différence 2. Puis, éliminez deux nombres de somme 12 et de produit 32.
Ensuite, éliminez deux nombres de différence 7 et de produit 78. Enfin,
éliminez deux nombres tels que quand on divise l'un par l'autre, le
quotient est 3 et le reste 2.
Quel est le nombre restant?
Début catégories C2 L1 L2 GP HC
- 5 - Le mot le plus court
(coefficient 5)
- Le petit Ababa joue avec les lettres de son alphabet. Il s'est
inventé les règles suivantes:
- si dans un mot, il trouve un A suivi d'un B, il peut les remplacer
par la séquence BAA
- si dans un mot, il trouve deux B qui se suivent, il peut les retirer
du mot
- si dans un mot, il trouve trois A qui se suivent, il peut les retirer
du mot.
En partant du mot ABABABAABAAB, quel est le mot le plus court qu'il
puisse obtenir?
- 6 - Le petit enclos
(coefficient 6)
- Pour réaliser un enclos sur un quadrillage, on pose des carrés
noirs sur les carrés du quadrillage, de façon à entourer un ou plusieurs
carrés du quadrillage. Les carrés noirs de l'enclos peuvent se toucher
par un côté ou par un sommet.
Avec 4 carrés noirs, on peut enclore un carré du quadrillage
(figure 1).
Avec 6 carrés noirs, on peut enclore 2 carrés du quadrillage
(figure 2).
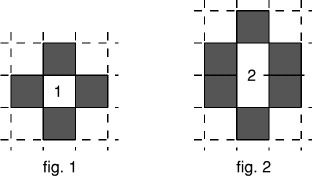
Quel est le nombre maximum de carrés du quadrillage que l'on peut
enclore avec 9 carrés noirs?
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Le C.D.
(coefficient 7)
- Le dernier C.D. des Math'Singers coûte un nombre
entier de francs.
Bien que sa tirelire ne soit pas vide, Mathias ne peut se l'offrir, car
il lui manque 47 F. Il en est de même
pour Mathilde, à qui il manque 2 F
pour se le payer.
Mathilde et Mathias décident alors de mettre leur argent en commun,
mais hélas, ils n'ont pas encore assez pour l'acheter.
Combien coûte le C.D. des Math'Singers?
- 8 - Famille nombreuse
(coefficient 8)
- Anne dit:
Je suis la sixième enfant de ma famille et j'ai au
moins autant de frères que de soeurs
. Son frère cadet Jean ajoute:
Moi par contre, j'ai au moins deux fois plus de soeurs que de
frères
.
Combien la famille d'Anne et de Jean compte-t-elle de filles et de
garçons?
- 9 - Les saules
(coefficient 9)
- Le bord d'un étang circulaire est planté de 5 magnifiques saules,
sur les branches desquels se trouvent des moineaux dont le nombre total
n'atteint pas 30.
À un certain moment, un moineau est passé du 1er saule au
second. Deux moineaux sont ensuite passés du second saule au troisième,
puis trois du troisième au quatrième, quatre du quatrième au cinquième,
et enfin cinq moineaux se sont déplacés du cinquième saule au premier.
Après ce manège, il y avait exactement le même nombre de moineaux sur
chacun des cinq saules.
Donnez les nombres d'oiseaux perchés sur chacun des arbres avant
qu'ils ne se déplacent.
Fin catégorie C1
- 10 - Les neuf nombres
(coefficient 10)
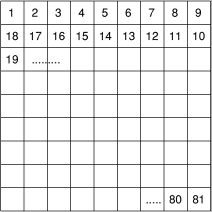
On inscrit les nombres de 1 à 81 dans les cases du tableau carré, en
procédant comme indiqué sur la figure. On choisit ensuite 9 nombres dans
ce tableau tels que 2 quelconques de ces neuf nombres n'appartiennent
jamais à une même ligne ni à une même colonne.
Quelle est la plus grande valeur possible de la somme de ces neuf
nombres?- 11 - Les cinq joueurs
(coefficient 11)
- Cinq joueurs A, B, C, D, E, jouent à la courte-paille. Avant chaque
partie, chacun des 5 joueurs mise une certaine somme d'argent qu'il pose
devant lui. Au départ, A mise plus que B, qui mise plus que C, qui mise
plus que D, qui mise plus que E. Chaque partie permet de déterminer un
perdant. Ce perdant doit doubler la mise de tous les autres joueurs, en
prenant sur sa propre mise, ou, si cela n'est pas suffisant, dans son
portefeuille, ce qui l'oblige alors à quitter le jeu.
Après 5 parties successives, aucun des 5 joueurs n'a abandonné, et chacun
a devant lui la somme de 32 F. Chaque
joueur a perdu exactement une fois. Quelles étaient, dans l'ordre de
A à E, les mises initiales des 5 joueurs?
Fin catégorie C2
- 12 - Que de 1!
(coefficient 12)
- Si je calcule
1
+ 11
+ 111
+ 1111
..............
+ 1111111111111...........111111111111
(dans la 96e et dernière ligne, le chiffre 1 est répété 96
fois), combien de chiffres 1 apparaîtront dans le résultat?
- 13 - Le grand sinus
(coefficient 13)
- Donnez la plus petite valeur de n pour laquelle l'expression
sin 2n, où n est un entier naturel, et où 2n
désigne la mesure d'un angle exprimée en degrés, prend la plus grande
valeur possible.
- 14 - Un coup d'éponge
(coefficient 14)
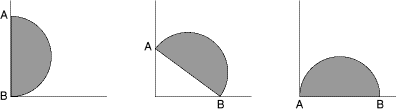
Une éponge semi-circulaire a pour diamètre
20 cm (voir figure, vue du dessus).
On fait glisser cette éponge, imbibée de produit nettoyant, sans la
presser, sur le sol, dans l'angle d'une pièce, de telle sorte que le
diamètre [AB] demeure constamment en contact avec les deux côtés de
l'angle droit.
Quelle sera l'aire nettoyée (on donnera cette aire
en cm², arrondie
au cm² le plus
proche) ?
Fin catégories L1 GP
- 15 - Le carré tétraédrique
(coefficient 15)
- Une boîte en carton a la forme d'un tétraèdre. On découpe cette
boîte selon trois arêtes issues d'un même sommet, et, en mettant les
faces à plat, on obtient un patron du tétraèdre. Or, ce patron est un
carré de côté 30 cm.
Quel était le volume de la boîte de départ?
- 16 - Le terrain du père Nissieux
(coefficient 16)
- Le père Nissieux, Victor, possède près de Lyon un terrain
ayant la forme d'un pentagone non régulier. Ce pentagone a deux
grands côtés consécutifs perpendiculaires mesurant chacun
100 m de long, et trois côtés
plus petits de même longueur. L'un de ces trois petits côtés est
parallèle à un des deux grands côtés. D'autre part, le terrain
de Victor a une aire d'un demi-hectare.
Quel est le périmètre du terrain de V. Nissieux?
On donnera ce périmètre arrondi au mètre le plus proche.
On pourra prendre, si besoin est, 1,414 pour
√2, 1,732 pour
√3, 2,236 pour
√5, 2,646 pour
√7.
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org