10^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 2^e séance, 31 août 1996

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Les 2 messages (coefficient 1)

Thomas a reçu un message, mais la machine défectueuse a omis une ou deux barres de chaque lettre de ce mot écrit en script:

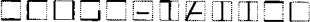
Son correspondant, se rendant compte que sa machine mange certains mots, renvoie le même message à Thomas, en espérant que ce deuxième message complétera le premier... Hélas, le même mot est transmis ainsi:

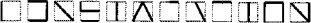
Aidez Thomas à reconstituer ce mot.

2 - Les émetteurs (coefficient 2)

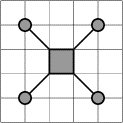
Vous disposez d'émetteurs constitués d'une unité centrale et de 4 antennes (voir figure ci-contre). Ces émetteurs doivent être placés dans la zone quadrillée ci-dessous de façon que l'unité centrale coïncide parfaitement avec un carré du quadrillage. Les émetteurs doivent être entièrement contenus dans le quadrillage (y compris les antennes), et deux émetteurs ne doivent jamais se toucher (même par les antennes).

Combien pouvez-vous en placer, au maximum, dans la zone quadrillée? Dessinez-les.

Début catégorie C1

3 - L'oeil du cyclope (coefficient 3)

Le petit Kevin a toujours peur de se tromper, aussi a-t-il toujours avec lui une table de multiplication.

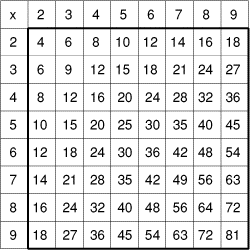
Son frère Mathias aime lui poser des énigmes. Il a fabriqué un cache carré en carton, avec un trou au centre.

Le cache couvre exactement 9 cases de la table de multiplication, laissant un nombre lisible en son centre. Mathias annonce à Kevin qu'il a caché 8 nombres dont la somme est 288. Il lui demande alors quel est le nombre visible au centre du cache. Aide Kevin!

4 - Labyrinthe (coefficient 4)

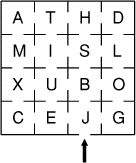
Je rentre les yeux bandés dans ce labyrinthe constitué de 4 fois 4 pièces disposées comme l'indique le plan. Sitôt franchie la première porte (qui donne dans la pièce J), je longe à tâtons le mur situé sur ma gauche, jusqu'à ce que je trouve une nouvelle porte. Je franchis alors cette porte, puis je longe aussitôt le mur situé à ma droite, jusqu'à ce que je trouve à nouveau une porte. Je franchis cette porte, et je longe ensuite le mur de gauche. Je continue ainsi, en longeant alternativement le mur de gauche et le mur de droite, le changement de côté s'effectuant à chaque franchissement d'une porte.
Écrivez la suite des pièces traversées depuis mon entrée dans le labyrinthe jusqu'à ma sortie du labyrinthe.

Début catégories C2 L1 L2 GP HC

5 - Mélancolie (coefficient 5)

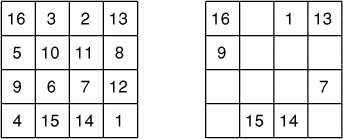
Le grand graveur Albrecht Dürer a prouvé ses connaissances arithmétiques dans une célèbre gravure intitulée Melencolia. En effet, dans un coin de l'oeuvre se trouve un carré magique d'ordre quatre... et, comble de raffinement, sur la dernière ligne apparaît le nombre 1514, qui est l'année de sa création! Vous pourrez vérifier que la somme des nombres sur les lignes, les colonnes et les deux diagonales, est toujours la même.
Vous pouvez faire aussi bien que Dürer en complétant à l'aide de tous les nombres compris entre 1 et 16 le carré magique ci-contre, différent, mais ayant la même somme magique.

6 - Les dominos de Dominique (coefficient 6)

Le grand-père de Dominique est un baroudeur. Il a bourlingué autour du monde, et a, jadis, rapporté à Dominique un jeu de dominos très spécial. Ce jeu comporte en effet tous les nombres de points de 0 à 9. Hélas, le désordre dans la chambre de Dominique est tel que dans le jeu, il n'y a plus que les 15 dominos représentés ci-contre!

Mais ces quinze dominos sont cependant rangés dans une boîte rectangulaire comme dans le dessin ci-dessous, dans lequel le domino 4 - 1 est déjà placé.

Pouvez-vous indiquer comment ils sont disposés dans la boîte?
Vous représenterez par un trait la séparation entre deux dominos.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Labyrinthe numérique (coefficient 7)

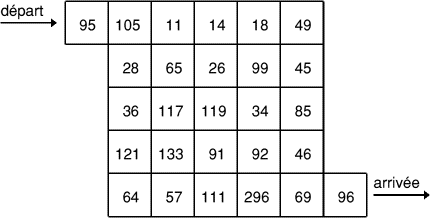
Vous entrez dans ce labyrinthe à la case marquée 95, et vous devez en sortir à la case marquée 96.
On ne peut passer d'une case à une case immédiatement voisine (se touchant par un côté) que si les nombres marqués sur ces deux cases peuvent se diviser exactement par un même nombre autre que 1 (on peut dire que ces deux nombres sont deux multiples d'un même nombre).
Indiquez par un trait le chemin que vous devez suivre.

8 - Quatre-vingt-dix-neuf (coefficient 8)

1 2 3 4 5 6 7 8 9
Dans cette suite des neuf chiffres de 1 à 9, on peut obtenir différents nombres, juste en intercalant des signes d'addition.
Par exemple: 1234 + 567 + 89 = 1890,
ou bien 1 + 23 + 4 + 56 + 7 + 89 = 180
En intercalant uniquement des signes d'addition, obtenez un total de 99!
Vous écrirez les signes + sur le bulletin-réponse.

9 - Palindrome d'un doute (coefficient 9)

Dans le film Tandem de Patrice Leconte, l'acteur Jean Rochefort observe le compteur kilométrique de sa voiture, 83 238, et dit que c'est un nombre palindrome: on peut le lire aussi bien de droite à gauche que de gauche à droite. Puis il remarque que le prochain nombre palindrome affiché par son compteur sera 83 338.
Dites-nous quel sera le septième après 83 338?

Fin catégorie C1

10 - Maître Fibo se déchaîne (coefficient 10)

Maître Fibonacci soumit un jour à son ami forgeron le problème suivant.
Voici dix fragments de chaîne. Deux sont constitués d'un seul anneau, mais les autres comptent respectivement 2, 3, 5, 8, 13, 21, 34 et 55 anneaux. Je voudrais utiliser tous ces anneaux pour constituer plusieurs chaînes toutes de même longueur (ayant le même nombre d'anneaux), et ouvertes, c'est-à-dire non refermées en boucle.
Le forgeron met 1 minute pour ouvrir et refermer un anneau.
Combien lui faudra-t-il de temps, au minimum, pour répondre aux voeux de Maître Fibo?

11 - Les années presque parfaites (coefficient 11)

1996 est une année presque parfaite, car l'un des nombres de 3 chiffres obtenus en supprimant l'un des chiffres de 1996 est un carré parfait. En effet, en enlevant l'un des 9, on obtient 196, qui est le carré de 14.
Avant 1996, combien y a-t-il eu d'années presque parfaites dans les années mille neuf cent?

Fin catégorie C2

12 - Le damier en morceaux (coefficient 12)

Découpez ce damier en plusieurs morceaux de telle sorte que:

• chaque morceau soit constitué d'un nombre entier de cases
• les nombres de cases des morceaux soient tous différents
• le nombre de cases du plus grand morceau soit le plus petit possible.

Donnez la somme des nombres de cases du plus petit et du plus grand morceau.

13 - Le grand enclos (coefficient 13)

Pour réaliser un enclos sur un quadrillage, on pose des carrés noirs sur les carrés du quadrillage, de façon à entourer un ou plusieurs carrés du quadrillage. Les carrés noirs de l'enclos peuvent se toucher par un côté ou par un sommet.
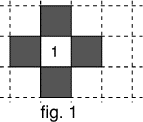
Avec 4 carrés noirs, on peut enclore au maximum 1 carré du quadrillage (figure 1).

Avec 6 carrés noirs, on peut enclore au maximum 2 carrés du quadrillage (figure 2).

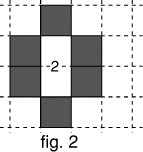
Quel est le plus grand nombre n de carrés noirs, tels qu'avec ces n carrés noirs, il ne soit pas possible d'enclore n carrés du quadrillage?
Répondez 0 si vous pensez qu'un tel nombre n n'existe pas.

14 - Les jacinthes de Jordi (coefficient 14)

On a demandé à Jordi Nié, le jardinier, de mettre en terre 6 oignons de jacinthe en respectant les conditions suivantes:

• trois oignons quelconques pris parmi les six ne doivent jamais être alignés
• parmi tous les triangles dont les trois sommets coïncident avec des oignons de jacinthe, on doit avoir le plus grand nombre possible de triangles rectangles.

Dites combien l'astucieux Jordi, qui n'est pas niais, a obtenu de triangles rectangles.

Fin catégories L1 GP

15 - Problème à boire (coefficient 15)

Monsieur Sylvain Aibon fait la tournée de ses amis. Étant chez son cher Boissansoif (en B), il doit se rendre chez Meurdesoif (en M), mais se rappelle que passer chez Cuvédort (en C) ne le rallongerait que de 1996 pas. Entre ces trois demeures bénies des dieux, les routes sont droites et le triangle BMC est rectangle en C et a des côtés qui sont des nombres entiers de pas. Sachant que Sylvain n'a jamais marché plus de 10 000 pas, dites-nous combien de pas séparent les caves de Boissansoif et de Meuredesoif.

16 - Le fond de la piscine (coefficient 16)

On veut recouvrir le fond d'une piscine avec des carrés de 50 cm de côté. Ces carrés sont soit blancs, soit bleus, mais il n'y en a pas le même nombre de chaque couleur.
La piscine est rectangulaire, mais non carrée. Tous les carrés d'une couleur constituent un rectangle centré, les carrés de l'autre couleur formant une bordure de largeur constante autour de lui. Tous les carrés sont entiers, et le fond est entièrement recouvert.

En utilisant exactement les mêmes carrés, on peut mettre les carrés bleus au centre et les carrés blancs autour, ou l'inverse!
Quelle est, au minimum, l'aire du fond de cette piscine, exprimée en dm²?

Fin catégories L2 HC