13e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 1re séance, 27 août 1999
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Le peigne de Mathias
(coefficient 1)
- Mathias vient de s'acheter un peigne. Curieux, il observe
que les grosses dents du peigne sont espacées de
7 mm, tandis que les dents fines
ne sont espacées que de 3 mm.
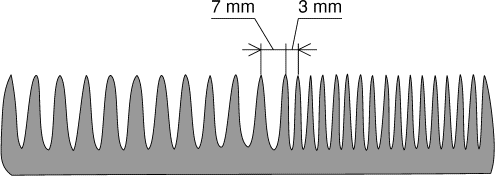
Trouvez deux dents du peigne de Mathias dont les extrémités sont
distantes d'exactement 32 mm.
Note: le dessin ci-dessus n'est pas à l'échelle.
- 2 - Remplissage
(coefficient 2)

On dispose de trois jetons bleus et de deux jetons rouges et on doit
placer un jeton par case dans le tableau ci-dessus en respectant les
règles suivantes:
- les deux jetons rouges ne doivents pas être voisins;
- deux des jetons bleus se suivent, mais pas les trois.
De combien de façons peut-on placer les cinq jetons en respectant
ces conditions?
Début catégorie C1
- 3 - Six nombres à placer
(coefficient 3)
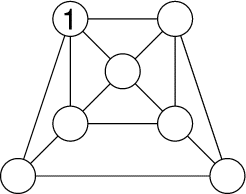
Placez les nombres de 2 à 7, de telle sorte que la différence
entre deux nombres directement reliés par un segment soit toujours
plus grande que 1.- 4 - L'escamide
(coefficient 4)
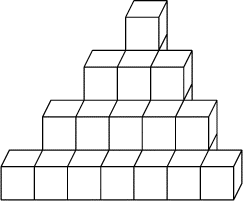
Thomas Thématik a construit avec des cubes une curieuse pyramide en forme
d'escalier. La largeur des marches diminue de deux cubes à chaque fois
que l'on monte d'une marche, jusqu'à la dernière marche qui ne compte
qu'un seul cube. Un exemple est représenté ci-contre avec quatre marches,
mais la pyramide de Thomas en compte huit.
Combien de cubes Thomas a-t-il utilisé?
Début catégories C2 L1 L2 GP HC
- 5 - Les hexagones roulants
(coefficient 5)
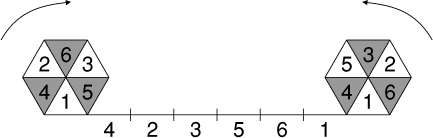
On numérote les cases de deux hexagones qui peuvent rouler en pivotant
sur les cases d'une droite elles aussi numérotées (voir figure).
Lorsqu'une case d'un hexagone vient sur une case de la droite, on
effectue le produit des deux nombres en contact. Par exemple, si
l'hexagone de gauche pivote pour venir sur la première case numérotée,
on effectue 5 × 4. On peut faire rouler
un hexagone,
ou les deux, chacun dans le sens indiqué par la flèche, et du nombre de
cases que l'on veut, jusqu'à ce qu'ils se touchent.
Si l'on additionne tous les produits obtenus, combien peut-on obtenir,
au maximum?- 6 - Puzzle tricolore
(coefficient 6)
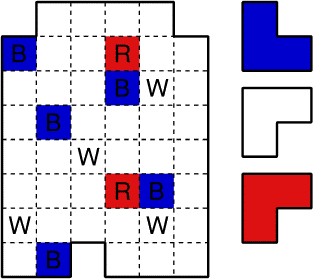
Nina a trouvé un vieux puzzle dans une malle du grenier de ses
grands-parents. Il s'agit de remplir la boîte ci-contre avec des pièces
en forme de V. Il y a 5 pièces bleues (B), 5 pièces blanches (W) et
5 pièces rouges (R). Facile!
, dit Thomas, le frère de Nina.
Oui, mais cela l'est moins si on veut que deux pièces de la même
couleur ne se touchent jamais par un côté!
, rétorque Nina.
À vous de trouver une solution du puzzle de Nina.
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Le trésor de Jules le Carré
(coefficient 7)
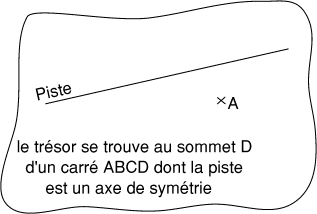
Jules était un vieux baroudeur qui avait beaucoup bourlingué.
Aussi avait-il caché son trésor dans un désert.
Avant de mourir, il a laissé à ses enfants, Jim et Julien,
un document précieux (ci-contre).
En combien d'endroits Jim et Julien doivent-ils prévoir de creuser
s'ils veulent être certains de récupérer le trésor de Jules?- 8 - Salade de fruits
(coefficient 8)
 |
F |
J |
M |
R |
|---|
| F |
J |
R |
M |
F |
|---|
| J |
R |
F |
J |
M |
|---|
| M |
M |
J |
F |
R |
|---|
| R |
F |
M |
R |
J |
|---|
| Départ |
F | F | J | M |
|---|
| R | J | R | F |
| 1ère ligne |
F | R | M | M |
|---|
| 2ème ligne |
F | M | R | M |
|---|
| 3ème ligne |
J | R | R | F |
|---|
Nina a inventé un système permettant de construire une suite de fruits à
l'aide du tableau ci-contre (F: fraise; J: jujube; M: melon; R: raisin).
Elle est partie d'un système de départ constitué de deux lignes.
Puis elle a suivi la loi du tableau:
F sur R donne F
F sur J donne R
J sur R donne M
M sur F donne M, ce qui lui a donné la première ligne, et ainsi de suite,
les deux dernières lignes écrites donnant la suivante.
Quelle sera la 999ème ligne?- 9 - Les couloirs du temps
(coefficient 9)
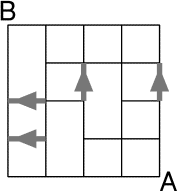
Voici le schéma d'un labyrinthe; vous êtes en A, et vous devez aller
en B en un temps minimum.
Chaque couloir ayant pour longueur le côté d'un petit carré unité
vous prend 10 secondes.
Chaque couloir noté à l'aide d'une flèche en trait épais est un couloir
du temps: si vous y entrez, vous êtes instantanément transporté à l'autre
extrémité! Combien existe-t-il de chemins permettant d'aller de A en B
en mettant le minimum de temps?
Fin catégorie C1
- 10 - La règle fautive
(coefficient 10)

Mathias vient de mesurer les longueurs des trois côtés du triangle qu'il
a construit. Il additionne ensuite les trois mesures, qui sont toutes des
nombres entiers de centimètres, et il obtient ainsi un périmètre égal à
15 cm. Le professeur, en passant,
lui indique que ce résultat est faux. Mathias n'a fait aucune erreur de
calcul, et il a utilisé correctement sa nouvelle règle, en effectuant
toutes ses mesures à partir du 0 de la graduation. Mais il réalise
soudain que la graduation de sa règle présente un petit défaut...
Quelles sont les longueurs (exactes) des trois côtés du triangle de
Mathias? On donnera les trois longueurs exprimées en centimètres,
dans l'ordre croissant.- 11 - L'escargot d'or
(coefficient 11)
- Chaque année, un
escargot d'or
, sculpture réalisée
par un artiste de renom, est offert au meilleur sprinter.
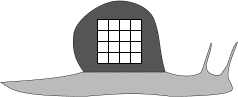
L'escargot d'or doit respecter la règle suivante.
Sur son côté droit se trouve un carré 4 × 4 constitué de 4 sortes
de pierres précieuses: émeraude, rubis, saphir, et diamant, à raison d'une
sorte de pierre sur chaque ligne, sur chaque colonne et sur chaque grande
diagonale. Les escargots d'or sont bien sûr tous différents. Pendant
combien d'années pourra-t-on attribuer un escargot d'or?
Fin catégorie C2
- 12 - La pyramide en bois
(coefficient 12)
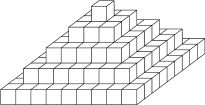
Un architecte a décidé, pour décorer une cité, de réaliser une pyramide
de cinq étages formée de cubes en bois tous identiques. L'architecte sait
qu'ensuite, il devra recouvrir le tout d'un épais vernis pour protéger
son oeuvre des intempéries.
Il fait faire une maquette au 1/5 d'un cube de la pyramide. Il constate
que ce cube réduit pèse 300 g, et que
lorsqu'il est entièrement recouvert de vernis, sa masse est de
306 g.
Quelle sera la masse de la pyramide une fois recouverte de vernis?
note: Seules les faces visibles de la pyramide seront vernies. On
négligera le vernis sur les arêtes.
Le résultat sera donné en kg, au gramme
près.- 13 - La scie à Simon
(coefficient 13)
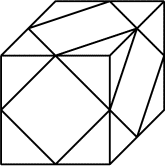
Simon, fana de bricolage, vient de s'acheter une nouvelle scie. Cet
outil, du dernier modèle, permet de faire des coupes parfaitement
planes et possède une lame tellement mince que les traits de scie
sont d'une épaisseur tout-à-fait négligeable.
Pour tester sa scie, Simon a pris un cube de bois et y a effectué plusieurs
coupes, sans bouger les morceaux entre deux coupes successives.
Il a alors obtenu le résultat représenté ci-dessus, les six faces du cube
ayant le même aspect.
Quel nombre de morceaux a-t-il pu obtenir au maximum?- 14 - Diviser pour multiplier
(coefficient 14)
- Julien a quelques problèmes avec les fractions. Il remplace la
barre de fraction par une virgule, et au lieu de multiplier, il divise.
Ainsi, pour multiplier 12 par 6 / 25, il divise 12 par 6,25.
Aujourd'hui, en procédant de la même façon pour multiplier un nombre
non nul par une fraction irréductible, il a obtenu le bon résultat.
Par quelle fraction Julien a-t-il multiplié le nombre?
Fin catégories L1 GP
- 15 - Le triangle
(coefficient 15)
- Un triangle rectangle a ses trois côtés qui mesurent chacun
un nombre entier de cm. On trace
à l'intérieur un cercle tangent à chacun des trois côtés dont le
rayon mesure exactement 3 cm.
Quelles sont les dimensions du triangle? On donnera les trois
longueurs exprimées en centimètres, dans l'ordre croissant.
- 16 - Le scribe indélicat
(coefficient 16)
- Un pharaon avait fait stocker un certain nombre de magnifiques
perles. Ce nombre, connu de tous, était considéré comme magique, ainsi
que tous ses diviseurs, les seuls autres nombres magiques.
Après la mort subite du pharaon, cinq voleurs, qui avaient repéré la
cachette, voulurent en profiter. Ils arrivèrent nuitamment et, l'un après
l'autre, chacun déroba le plus grand nombre de perles possible, ce nombre
étant magique... Le dernier voleur eut la surprise de ne trouver qu'une
seule perle!
Au petit matin, le scribe responsable du trésor, trouvant la cachette
vide, se félicita d'avoir détourné pour son propre compte, avant le
passage des cinq voleurs, un nombre de perles (non magique) correspondant
à trois centièmes du trésor!
Combien de perles le scribe indélicat avait-il dérobé?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org